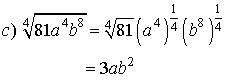|
 |
 |
 |
 |
|||||||||
|
|
|||||||||||||
UNIT 4 : EXPONENTIAL
& LOGARITHMIC FUNCTIONS
LESSON 1:
LAWS OF EXPONENTS
Examples of Powers:
25
= 2 x 2 x 2 x 2 x 2 = 32; (-3)3
= (-3) x (-3) x (-3) = -27; 2.72
= 2.7 x 2.7 = 7.29
A POWER (am
) consists of two parts; the base “a” and the exponent “m”.
Review of Basic Exponent Laws:
|
Rule |
Example |
Explanation |
|
am x an = am+n |
32 x 35 = 37 |
Multiplication Rule - If the bases are the same, add the exponents |
|
|
|
Division Rule - If the bases are the same, subtract the exponents |
|
(am)n
= amn |
(32)3=36 |
Power Rule – When taking a power of a power, multiply the exponents |
|
(ab)m
= amam |
(3 x 2)4 = 34
x 24 |
Power of a Product – Take each factor in the product to that power |
|
|
|
Power of a Quotient – Take numerator and denominator to that power |
Example 1: Simplify.
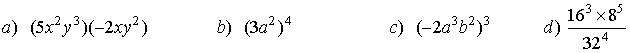
Solutions:




Example 2: Simplify.
![]()
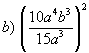
![]()
Solutions:


Example 3: Simplify each of the following:
![]()
![]()
![]()
Solutions:
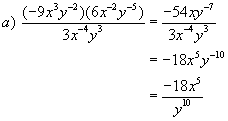
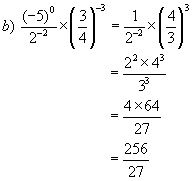

Alternate solution for c):

Rational
Exponents:
![]()
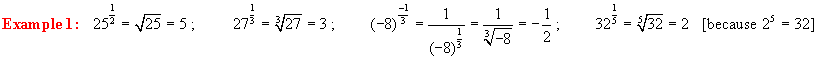
Review
of Radicals and Roots:
Example 2:





Example 4: Simplify
![]()

![]()
![]()
Solutions:
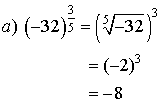

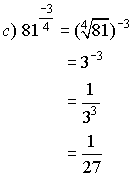

Example 5: Simplify
![]()
![]()
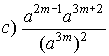
Solutions:



Example 6: Simplify
![]()
![]()
![]()
![]()
Solutions: