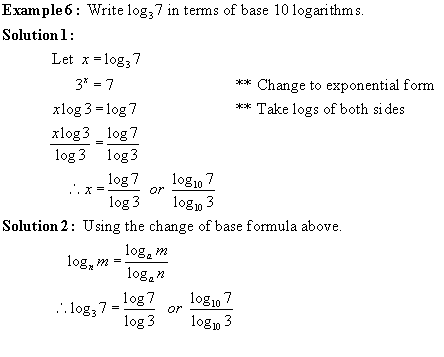|
|
|
|
|
|||||||||
|
|
|||||||||||||
UNIT
4 : EXPONENTIAL & LOGARITHMIC
FUNCTIONS
LESSON 6: LOGARITHMIC & EXPONENTIAL
EQUATIONS II
The following properties
of logarithms are important and used frequently in our study of
logarithms.
They correspond closely to
our rules for exponents studied earlier.


Note: When we
read log28, we ask the
question To what exponent must base 2
be raised to give 8? The answer is of
course 3
and this idea gives rise to the
following definition.
Definition:
the expression logax is defined to mean the exponent to which base a must
be raised to give x.
The expression reads:
the logarithm of x, base a.
Hence log10100 means the exponent to which
base 10 must be raised to give 100. The
answer is 2, giving the statement log10100
= 2.
Hence log381 means the exponent to
which base 3 must be raised to give 81.
The answer is 4, giving the statement
log381 = 4.
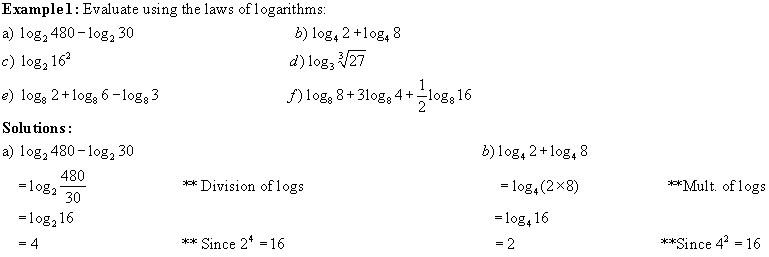

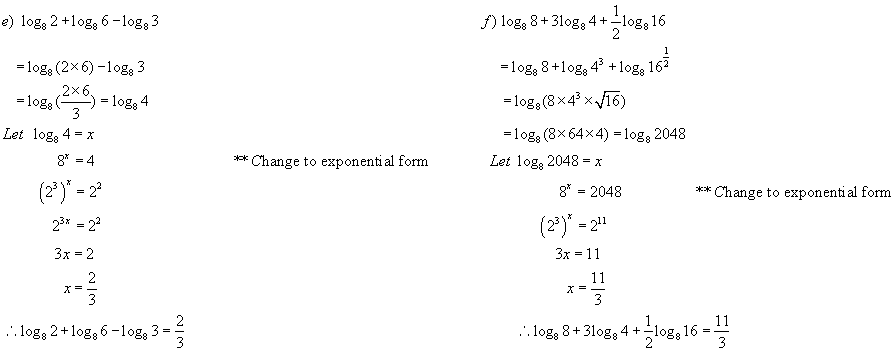
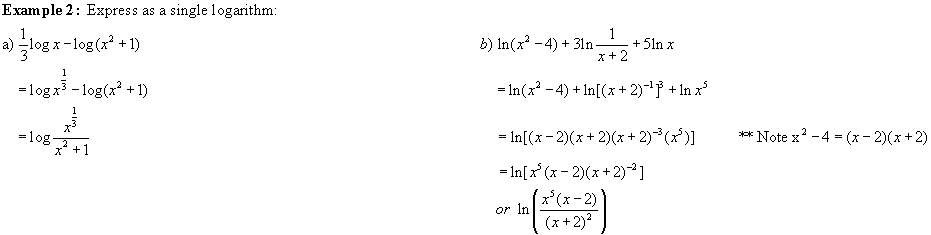

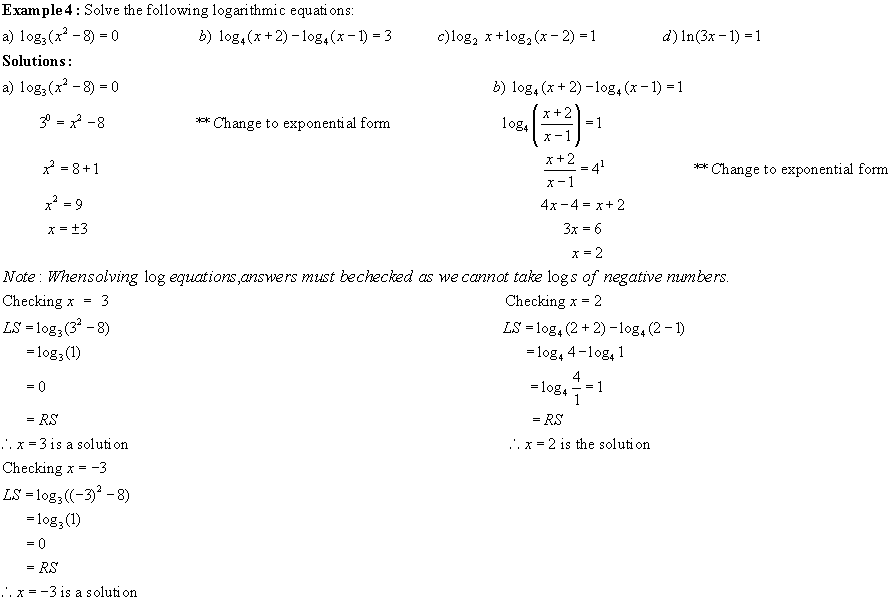
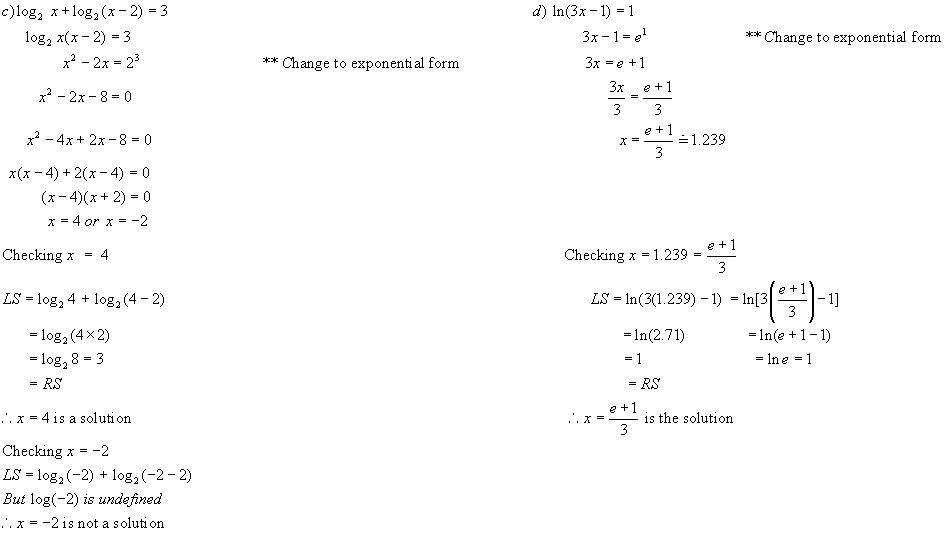
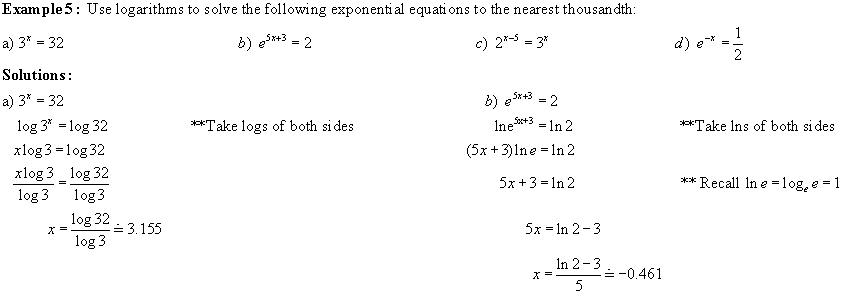
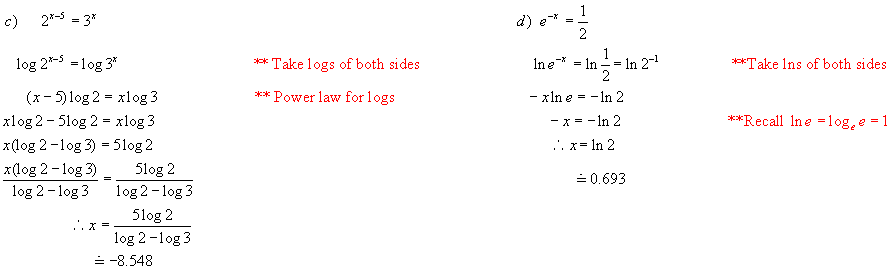
Note: See # 12 in homework questions for more
examples