Home

Exponents

Exponential Equations I

Exponential Functions

The Exponential Function Base e

The Logarithm Function

Logarithmic & Exponential Equations II

Applications:Growth & Decay

Review&Test

UNIT 4 : EXPONENTIAL & LOGARITHMIC FUNCTIONS

LESSON 2: EXPONENTIAL EQUATIONS

Exponential Equations:

Definition: An exponential equation is an equation where the variable is in the exponent.

Examples of Exponential Equations: 2^x = 64; 9^{2x – 1} = 729; 500(1.02)^{x – 1} = 897.56

Theorem: If a^x = a^y, then x = y. In words: If an exponential equation has the bases equal, then the exponents must be equal.

This theorem gives us our strategy for solving exponential equations, namely convert each side of the equation to a common base.

Note: Exponential equations may also be solved by taking logarithms of both sides of the equation. This method will be discussed in lesson 6

Example 1: Solve for x.

Solutions:

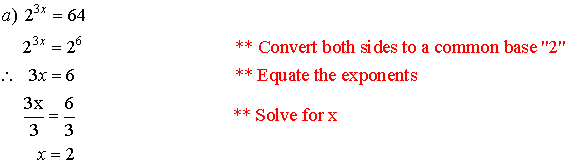
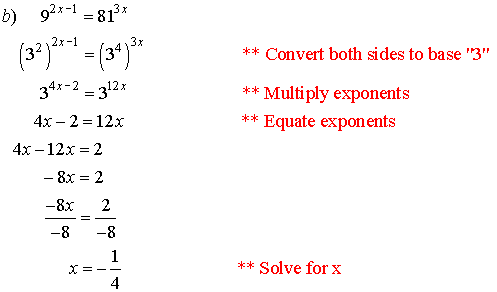
Example 2: Solve for x. Check # b.

Solutions:

APPLICATIONS:

Exponential Growth and Radioactive Decay are applications of exponential equations.

Example 1:

A bacteria culture doubles in size every 10 minutes. It’s growth is measured by the following formula:

, where

· A is the number of bacteria after the given time frame

· A₀ is the starting number of bacteria

· 2 is the growth factor

· t is the total time elapsed in the experiment

· d is the doubling period

How many bacteria will there be in the culture after 1 ½ hours if there were 20 bacteria in the original culture?

Solution:

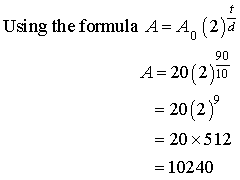
A = ?

A₀ = 20

t = 1 ½ h = 90 min

d = 10 min.

Therefore there will be 10 240 bacteria in the culture after 1 ½ hours.

Note: The half-life of a radioactive substance is the period of time a given amount will decay to half of it’s original amount.

Example 2:

The half-life of radioactive radon is 4 days. I t decays according to the formula below:

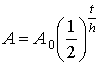, where

· A is the mass remaining after the decay period

· A₀ is the original mass of radioactive material

· ½ is the decay factor

· t is the total time elapsed

· h is the half-life of the material

If the amount remaining after 40 days is 6.5 g, calculate the original amount.

Solution:

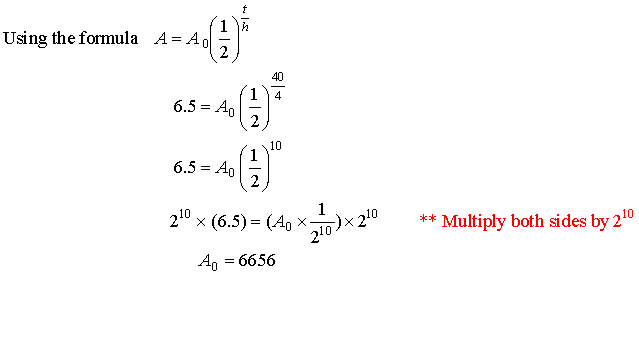
A = 6.5 g

A₀ = ?

t = 40 days

h = 4 days

Therefore the original mass was 6656 g.

Note: An equivalent formula for radioactive decay is:

Return to top of page

Click here to go to homework questions