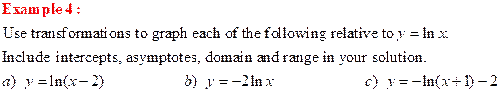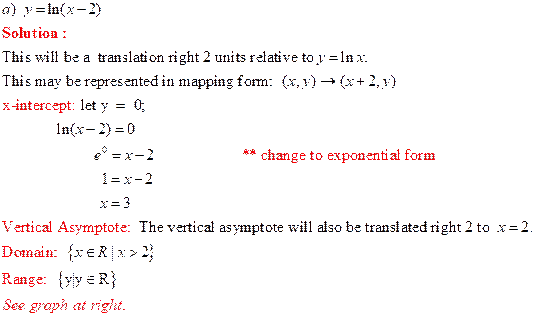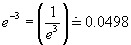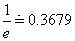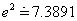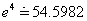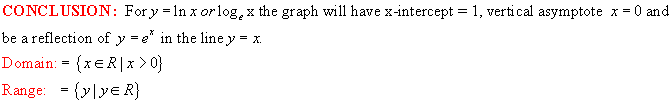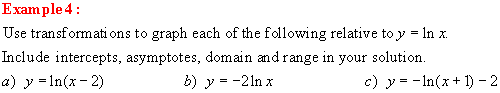|
|
|
|
|
|
|||||||||
|
|
|||||||||||||
UNIT 4 :
EXPONENTIAL & LOGARITHMIC FUNCTIONS
LESSON 5: THE LOGARITHMIC FUNCTION
Logarithmic
Notation:
The
exponential statement 23 =
8 may be rewritten in what is called
logarithmic form
as
follows: log28 = 3 which reads:
the logarithm of 8, base 2, equals 3.
Any
exponential statement may be rewritten in this form.
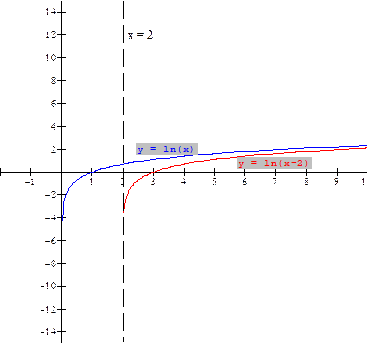
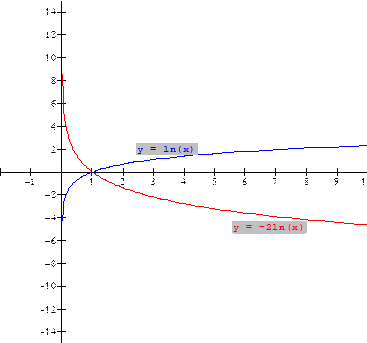
Example 1:
Complete the following chart by
converting between exponential and logarithmic form.
|
Exponential Form |
Logarithmic Form |
|
34 = 81 |
|
|
52 = 25 |
|
|
log232 = 5 |
|
|
log101000 = 3 |
|
|
|
|
|
|
Solution:
|
Exponential Form |
Logarithmic Form |
|
34 = 81 |
log381 = 4 |
|
52 = 25 |
log525 = 2 |
|
25 = 32 |
log232 = 5 |
|
103 = 1000 |
log101000 = 3 |
|
|
|
|
|
|
Note: When we read
log28, we ask the question
To what exponent must base 2 be raised to give 8? The answer
is of course 3 and this idea gives rise to the
following definition.
Definition: the expression logax is defined to mean the exponent to which base a must be
raised
to give x. The expression reads: the logarithm of
x, base a.
Hence log10100
means the exponent to which base 10 must be raised to give 100. The answer is 2, giving the
statement log10100
= 2.
Hence log381
means the exponent to which base 3 must be raised to give 81. The answer is 4, giving the
statement log381
= 4.
The
Logarithmic Function:
Logarithmic functions are the inverses of exponential
functions. How does this come
about?? See example below.
![]()
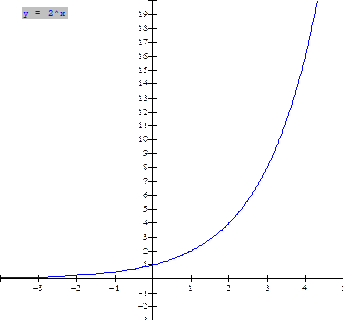
Table of Values & Graphs:
|
x |
y |
|
-3 |
|
|
-2 |
|
|
-1 |
|
|
0 |
1 |
|
1 |
|
|
2 |
|
|
3 |
8 |
|
4 |
16 |
Now form the
inverse of this function by interchanging x and y in the ordered pairs and the
equation.
|
x |
y |
|
|
-3 |
|
|
-2 |
|
|
-1 |
|
1 |
0 |
|
|
1 |
|
|
2 |
|
8 |
3 |
|
16 |
4 |
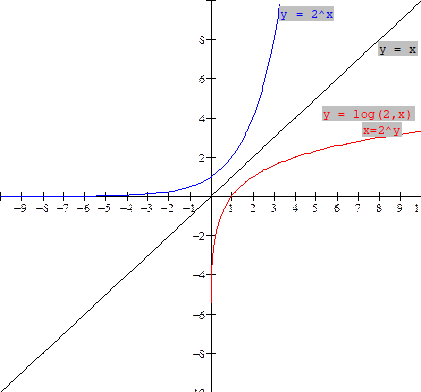
The equation of
the inverse is found by interchanging x and y in the equation y = 2x. This yields
x = 2y. If we put
this
equation in
logarithmic notation, we obtain the
logarithmic function y = log2x.
The graph is a
reflection in the line y = x of the exponential function y = 2x and
is shown in red above.
![]()

Table of Values & graph:
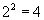
|
x |
y |
|
-3 |
|
|
-2 |
|
|
-1 |
3 |
|
0 |
1 |
|
1 |
|
|
2 |
|
|
3 |
|
![]()
Now form the
inverse of this function by interchanging x and y in the ordered pairs and the
equation.
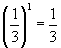
|
x |
y |
|
|
-3 |
|
|
-2 |
|
3 |
-1 |
|
1 |
0 |
|
|
1 |
|
|
2 |
|
|
3 |
The equation of
the inverse is found by interchanging x and y in the equation y = (1/3)x. This yields
x = (1/3)y. If we put
this
equation in
logarithmic notation, we obtain the
logarithmic function y = log(1/3)x.
The graph is a
reflection in the line y = x of the exponential function y = (1/3)x
and is shown in red above.
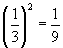
The
Natural Logarithmic Function y = logex or y =
ln x:
![]()
![]()
|
x |
|
|
-3 |
|
|
-2 |
|
|
-1 |
|
|
0 |
1 |
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
Now form the
inverse of this function by interchanging x and y in the ordered pairs above.
|
x |
y |
|
|
-3 |
|
|
-2 |
|
|
-1 |
|
1 |
0 |
|
|
1 |
|
|
2 |
|
|
5 |
|
|
4 |
The equation of
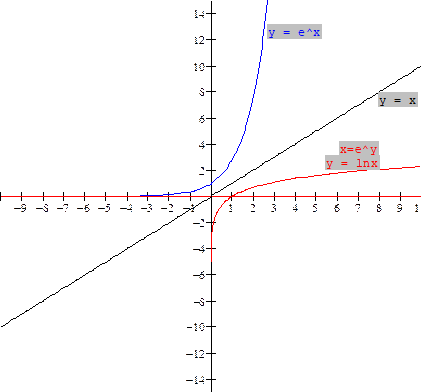
the inverse is found by interchanging x and y in the equation y = ex. This yields
x = ey. If we put
this
equation in
logarithmic notation, we obtain the
logarithmic function y = logex or y = lnx.
The graph is a
reflection in the line y = x of the exponential function y = ex and
is shown in red above.