|
|
|
|
|
||||||||
|
|
||||||||||||
|
|
UNIT
11 :
MATHEMATICS OF INVESTMENT
LESSON 6:
MORTGAGES
Example 1:
a) Camille has just purchased a new
house near Brantford. She needs a
mortgage of $150 000 after her down payment..
She will repay it in monthly instalments over 25 years.
The
interest rate is 6.6%/a, compounded semi-annually. Find the monthly payment.
b) Determine the total interest paid over the
25 year period.
Solution:
Here the
payment interval( monthly ) is different than the interest period (
semi-annual). This is a general annuity.
We must
match the interest period to the payment interval.
Ie. We
must find the monthly rate that is equivalent to 6.6%/a, compounded
semi-annually.
Step 1:
Using the formula A = P(1 + i)n,
find the value of $1 invested at 6.6%/a, compounded semi-annually after 1 year.
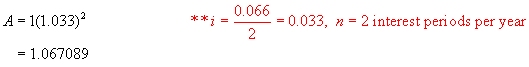
Step 2:
Let the equivalent monthly rate be i %. (Note the equivalent yearly rate would be 12i %.)
Now find the value of $1 invested at i % per month after 1 year.
A = 1(1 + i)12 ** n = 12, the number of times interest is
compounded per year.
Step 3:
These two amounts must be equal.
Hence
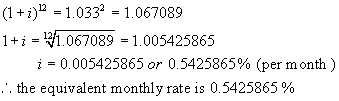
The money in question is borrowed now – at
point 0 on the time line. Hence this is
a PV general annuity question
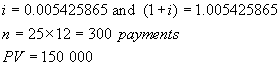
Interest Period 0 1 2 3 298 299 300
Payment R
R R R R R
R(1.005425865)-1
R(1.005425865)-2
.
.
R(1.005425865)-298
R(1.005425865)-299
R(1.005425865)-300
This
forms the following geometric series:
R(1.005425865)-300 +
R(1.005425865)-59 + . . . + R(1.005425865)-2 +
R(1.005425865)-1
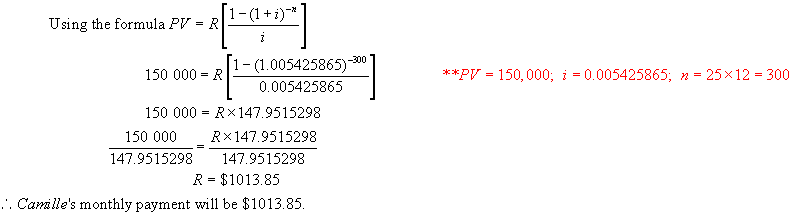
b)
Determine the total interest paid over the 25 year period.
Total amount repaid = 1013.85 x 300
= $304 095.00
Mortgage amount = $150 000
Interest paid = $304 095 - $!50
000 =$154 095
Hence
the total interest paid over 25 years is $154 095.