|
|
|
|
|
||||||||
|
|
||||||||||||
|
|
UNIT
9 :
MATHEMATICS OF INVESTMENT
LESSON 3:
ORDINARY ANNUITIES
Definition: A sequence
of payments made at
regular intervals is called an annuity.
![]()
![]()
![]()
![]()
![]()
![]()
![]() Interest Period 0
1 2 3 18
19 20
Interest Period 0
1 2 3 18
19 20
![]()
Payment 200 200 200 200 200 200
An ordinary annuity has the following properties.

![Text Box: P = principal [amount borrowed
or invested]
n = number of interest periods
i = interest rate per interest period as
as a decimal
A = accumulated amount (due or payable)](./ordann_files/image011.gif)
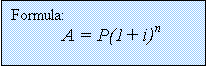


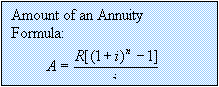
Example 1: Finding the accumulated amount of an annuity.
Laura
plans to save for her retirement by investing $200 every month. How much will she have after 20 years if
interest is 6%/a, compounded monthly?
Include a time line diagram in the solution.
Solution:
![]()
![]()
![]()
![]()
![]()
![]()
![]() Interest period0 1 2 . . . 238 239
240 Accumulated value
Interest period0 1 2 . . . 238 239
240 Accumulated value
Payment 200 200 200 200 200
![]()
![]()
![]()
![]()
![]()
![]() 200
200
![]() 200(1.005)1
200(1.005)1
![]() 200(1.005)2
200(1.005)2
.
.
.
![]() 200(1.005)238
200(1.005)238
![]() 200(1.005)239
200(1.005)239
There
are 12 x 20 = 240 payments over the term of the annuity. The first payment
occurs at the end of the first month as in the diagram. The last payment occurs on the last day of
the 240th month and collects no interest as we evaluate the series
at that point. We evaluate each term of the series separately
using the formula A = P(1 + i)n

Hence
Laura will have accumulated $92 408.18 after 20 years.
Example 2: Finding the regular payment of an annuity.
Tanya
plans to save for her retirement by investing a fixed amount once a year. How much should she invest each year if she
wishes to have $150 000 available after 35 years and interest is 8%/a, compounded annually? Include a time line diagram in the solution.
Solution:
Let the
yearly payment Be $R, with the first payment at the end of the first year.
![]()
![]()
![]()
![]()
![]()
![]()
![]() Interest period0 1
2 . . . 33 34
35 Accumulated
value
Interest period0 1
2 . . . 33 34
35 Accumulated
value
Payment R R
R R R
![]()
![]()
![]()
![]()
![]()
![]() R
R
![]() R(1.08)1
R(1.08)1
![]() R(1.08)2
R(1.08)2
.
.
.
![]() R(1.08)33
R(1.08)33
![]() R(1.08)34
R(1.08)34
There
are 35 payments over the term of the annuity. The first payment occurs at the
end of the first year as in the diagram.
The last payment occurs on the last day of the 35th year and
collects no interest as we evaluate the series at that point. We evaluate each
term of the series separately using
the formula
A = P(1 + i)n