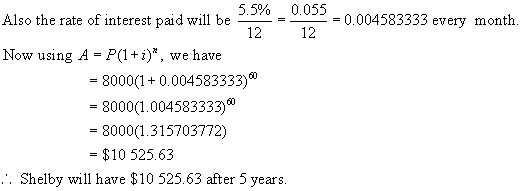|
|
|
|
|
||||||||
|
|
||||||||||||
|
|
UNIT
9 :
MATHEMATICS OF INVESTMENT
LESSON 1:
SIMPLE AND COMPOUND INTEREST
Simple
Interest:
When you
borrow or invest money, interest is paid or earned. If the interest is calculated only on the money originally invested, it is called simple
interest.
![Text Box: I = interest due or earned
p = principal [amount borrowed
or invested]
t = time in years
r = yearly interest rate as a decimal
A = amount repayable or accumulated](./comp_files/image002.gif)
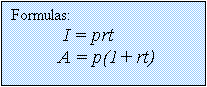
Example 1:
Jenna
borrows $5000 from her parents to start a landscaping business. She agrees to repay the loan in 3 years and
to pay simple interest at a rate of 5%/a [5% per annum]. Calculate the interest due in 3 years and
the total amount repayable.
Solution:
p = 5000 r = 0.05 t = 3 I = ? A = ?

Compound
Interest:
If
interest is calculated at the end of each year (or interest period) and added
on at this point, then this is called compound
interest.
![Text Box: P = principal [amount borrowed
or invested]
n = number of interest periods
i = interest rate per interest period as
as a decimal
A = accumulated amount (due or payable)](./comp_files/image006.gif)
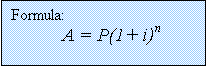
Example 2:
a) Suppose Jenna had borrowed the money from a
bank at 5%/a compounded yearly. This
means interest is calculated at the end of each year and added on. Hence at the end of the second year you
would be paying interest on the original amount and interest on the first
year’s interest as well. This is compound interest.
Solution:
p = 5000 n = 3 i = 0.05 A = ?
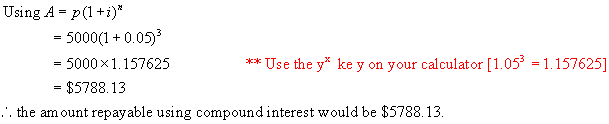
b) How much interest did Jenna pay?
Solution:
Subtract
the amount repayable from the principle.
Interest = $5788.13 - $5000 =
$788.13
Time
Value of Money:
The
investment above can be illustrated on a time line. Time = 0 means today. The
arrow moving to the right shows the investment increasing over the 3 year
period.
![]()
![]()
![]()
![]() 0 1 2 3
0 1 2 3
![]()
![]()
![]() $5000 $5000(1.05)3
$5000 $5000(1.05)3
Note: We can evaluate a give sum of money at any point using a
time line simply using the compound interest formula, the correct interest rate
and the correct number of time periods.
Example 3: Using different compounding periods.
a) Shelby invested $8 000 in a 5-year term
deposit which pays interest at a rate of 5 %/a [per annum], compounded
semi-annually. What will the investment
be worth at the end of the 5 year period?
Solution:
Because
the interest is compounded every 6 months, we must adjust both the number of
interest periods n and the interest rate i.
If
interest is paid twice a year, then the number of interest periods [compounding
periods] will be 5 x 2 = 10. Hence n
= 10.
The
appropriate time line is shown below.
Since there are 10 interest periods, we will put a mark every 6 months
over the 5-year period.
0 1 2 . .
. . . 4
5
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() …
…
![]() $8000 $8000(1.025)10
$8000 $8000(1.025)10
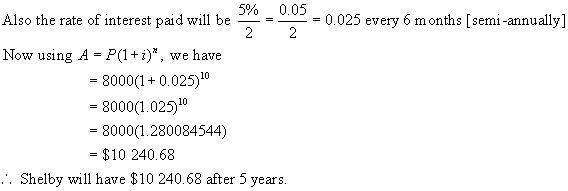
b) What will the investment be worth if
interest is 6.5%/a, compounded quarterly.
Solution:
Because
the interest is compounded every 3 months, we must adjust both the number of
interest periods n and the interest rate i.
If
interest is paid 4 times a year, then the number of interest periods
[compounding periods] will be 5 x 4 = 20.
Hence n = 20.
The
appropriate time line is shown below.
Since there are 20 interest periods, we will put a mark every 3 months
over the 5-year period.
0 1 . .
. . . 4
5
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() …
…
![]() $8000 $8000(1.01625)20
$8000 $8000(1.01625)20
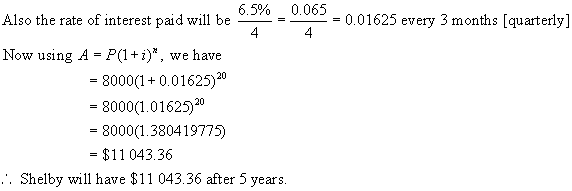
c) What will the investment be worth if
interest is 5.5%/a, compounded monthly.
Solution:
Because
the interest is compounded every month,
we must adjust both the number of interest periods n and the interest
rate i.
If
interest is paid 12 times a year, then the number of interest periods
[compounding periods] will be 5 x 12 = 60.
Hence n = 60.
The
appropriate time line is shown below.
Since there are 60 interest periods, we will number the line using
months.
0 1 2 3
4 . .
. . . 58
59 60 [5 years]
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() …
…
![]() $8000 $8000(1.004583333)60
$8000 $8000(1.004583333)60