|
|
|
|
|
||||||||||
|
|
||||||||||||||
UNIT 3 : QUADRATIC FUNCTIONS & EQUATIONS
LESSON
8: RECIPROCAL FUNCTIONS HOMEWORK
QUESTIONS
Quick Review :
1. For each of the following, sketch the graph and its reciprocal.
2. Given the function y = x – 2.
a) Sketch the graph and its reciprocal.
b) State the domain and range of the reciprocal.
c) Find the equation of the inverse of the reciprocal function.
3. Sketch the graph of the reciprocal function for each of the following.
a)
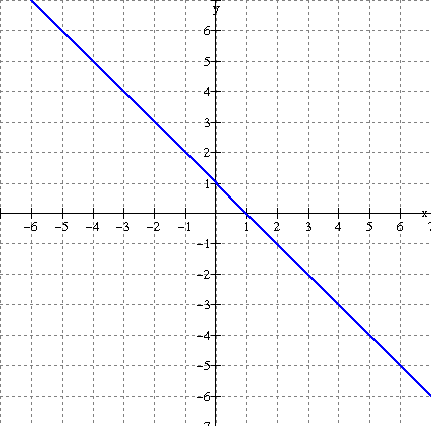
b)
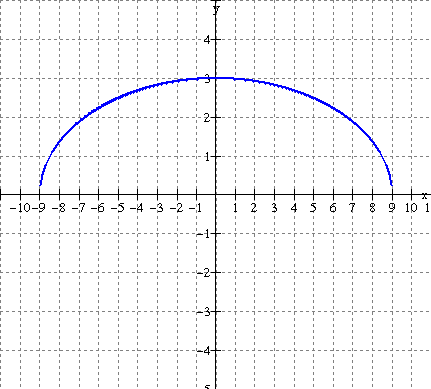
c)
Solutions:
1. For each of the following, sketch the graph and its reciprocal.
Solution:
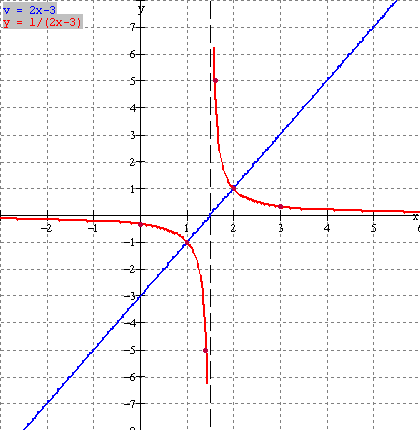
First
find the zeros or x – intercepts of y = 2x - 3. Let y = 0 and solve for x.
0 = 2x - 3
and
2x
= 3
x = 1.5
Hence x = 1.5
is the x – intercept of f(x) and the vertical
asymptote (VA) of the
reciprocal.
Now
graph the straight line using the x-intercept and points in table below. (blue graph below)
Find all
points on the line where y=1 or y=-1.
[(2, 1) and (1, -1)]
Now make
a table of values including points near the asymptote x = 1.5.
|
x |
|
|
|
-3 |
-9 |
-1/9= -0.11 |
|
-2 |
-7 |
- 1/7= -0.14 |
|
-1 |
-5 |
-1/5= -0.2 |
|
0 |
-3 |
-1/3= -0.33 |
|
1 |
-1 |
-1 |
|
1.4 |
-0.2 |
-1/0.2= -5 |
|
1.5 |
0 |
VA |
|
1.6 |
0.2 |
5 |
|
2 |
1 |
1 |
|
3 |
3 |
0.33 |
|
4 |
5 |
0.2 |
|
5 |
7 |
0.14 |
Note values of x taken near asymptote:
x
=1.4, 1.6
See
graph at left (red).
Solution:
First
find the zeros or x – intercepts. Let y
= 0 and solve for x.
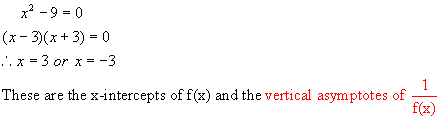
Next find
the vertex of the parabola f(x):.
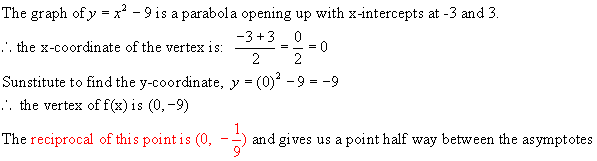
Now graph the parabola using the x-intercepts and vertex
calculated above. (blue graph below)
Find all
points on the parabola where y=1 or y=-1.
[approx. (3.05, 1), (-3.05, 1), and
(2.95, -1), (-2.95, -1)]
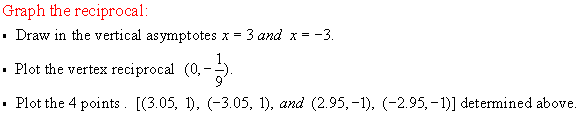
Now make
a table of values if needed including points near
the asymptotes x = -3 and x = 3.
|
x |
|
|
|
-5 |
16 |
1/16 |
|
-4 |
7 |
1/7 |
|
-3.5 |
3.25 |
0.31 |
|
-3.1 |
0.61 |
1.64 |
|
-3.01 |
0.0601 |
16.64 |
|
-3 |
0 |
Undef - VA |
|
-2.99 |
-0.0599 |
-16.69 |
|
-2.9 |
-0.59 |
-1.69 |
|
0 |
-9 |
-1/9 |
|
2.9 |
-0.59 |
-1.69 |
|
3 |
0 |
Undef - VA |
|
3.1 |
0.61 |
1.64 |
|
4 |
7 |
1/7 |
|
5 |
16 |
1/16 |
Note values of x taken near asymptotes:
x
= - 3.1, -3.01, - 2.9, -2.99, 2.9, 3.1
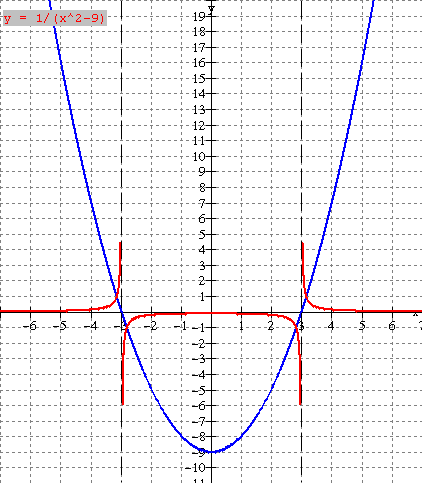
Please note the following from the graph and table:
·
The
graph of y = f(x) = x2 - 9 (blue) is a parabola with vertex at (0, -9) and zeros –3, 3. Its reciprocal (red) has 3 branches separated by the lines
x = - 3 and x
= 3(dashed).
·
Where
f(x) has a zero (x – intercept), the reciprocal has
an asymptote (x = - 3 and x = 3 (dashed))
·
The
behaviour near the asymptotes is interesting;
as x approaches - 3 from the right (x = -2.9, -2.99 in table), the
reciprocal (red) gets very large in the negative
direction (goes down); as x approaches
- 3 from the left (x = - 3.1, -3.01 in table), the reciprocal (red) gets very large in the positive direction (goes up). Similar behaviour occurs near the other
asymptote x = 3.
·
As x
takes on larger positive values (x = 5, 6 in table), the reciprocal takes on
smaller values approaching zero from above.
As x takes on larger negative values (- 3, - 4 in table), the reciprocal
takes on smaller values approaching zero again from above.
·
Where
f(x) is positive, the reciprocal is positive; where f(x) is negative, the reciprocal is
negative.
·
Where
f(x) = 1, the reciprocal equals 1;
where f(x) = -1, the reciprocal equals –1.
Solution:
First
find the zeros or x – intercepts. Let y
= 0 and solve for x.
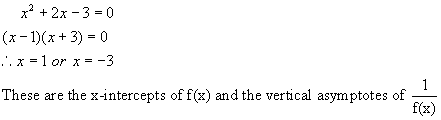
Next
find the vertex.
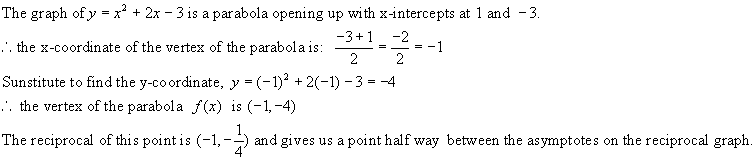
Now
graph the parabola using the x-intercepts and vertex calculated above. (blue graph below)
Find all
points on the parabola where y=1 or y=-1. approx. [(1.2, 1), (-3.2, 1), and (0.7, -1), (-2.7, -1)]
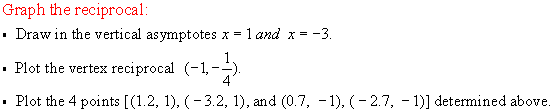
Now make
a table of values if needed including points near the asymptotes x = -3 and x =
1 if needed.
|
x |
|
|
|
-5 |
12 |
1/12 |
|
-4 |
5 |
1/5 |
|
-3.5 |
2.25 |
1/2.25 = 0.44 |
|
-3.1 |
0.41 |
2.44 |
|
-3.01 |
0.0401 |
24.94 |
|
-3 |
0 |
Undef.(VA) |
|
-2.99 |
-0.0399 |
-25.06 |
|
-2.9 |
-0.39 |
-2.56 |
|
-2 |
-3 |
-1/3 |
|
-1 |
-4 |
-¼ |
|
0 |
-3 |
-1/3 |
|
0.9 |
-0.39 |
-2.56 |
|
1 |
0 |
Undef.(VA) |
|
1.1 |
0.41 |
2.44 |
|
2 |
5 |
1/5 |
|
3 |
12 |
1/12 |
Note values of x taken near asymptotes:
x
= - 3.1, -3.01, - 2.9, -2.99, 0.9, 1.1
Please note the following from the graph and table:
·
The
graph of y = f(x) = x2 + 2x
- 3 (blue) is a parabola with vertex at (-1, -4) and
zeros –3, 1. Its reciprocal (red)
has 3 branches
separated by the lines x = - 3 and x =
1(dashed).
·
Where
f(x) has a zero (x – intercept), the reciprocal has
an asymptote (x = - 3 and x = 1 dashed)
·
As x
approaches - 3 from the right (x = -2.9, -2.99 in table), the reciprocal (red) gets very large in the negative direction (goes down).
·
As x
approaches - 3 from the left (x = - 3.1, -3.01 in table), the reciprocal (red) gets very large in the positive direction (goes up).
·
Similar
behaviour occurs near the other asymptote x = 1.
·
As x
takes on larger positive values (x = 2, 3 in table), the reciprocal takes on
smaller values approaching zero from above.
·
As x
takes on larger negative values (- 4, - 5 in table), the reciprocal takes on smaller
values approaching zero again from above.
·
Where
f(x) is positive, the reciprocal is positive; where f(x) is negative, the reciprocal is
negative.
·
Where
f(x) = 1, the reciprocal equals 1;
where f(x) = -1, the reciprocal equals –1.
2. Given the function y = x – 2.
a) Sketch the graph and its reciprocal.
b) State the domain and range of the reciprocal.
c) Find the equation of the inverse of the reciprocal function.
Solution:
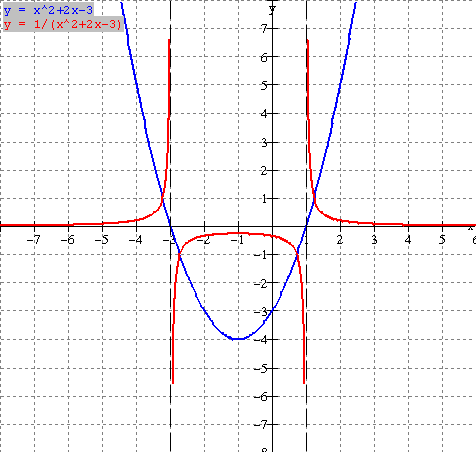
First
find the zeros or x – intercepts of y = x – 2. Let y = 0 and solve for x.
0
= x –2 and
x = 2
Hence x = 2 is the x – intercept of f(x) and the vertical
asymptote of the
reciprocal.
Now make
a table of values as in above example including values on either side of the
asymptote x = 2.
|
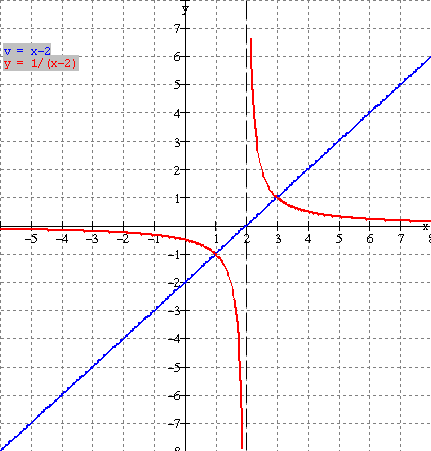
x |
|
|
|
-6 |
-8 |
-1/8 |
|
-1 |
-3 |
-1/3 |
|
0 |
-2 |
-½ |
|
1 |
-1 |
-1 |
|
1.5 |
-0.5 |
-2 |
|
1.9 |
-0.1 |
-10 |
|
1.99 |
-0.01 |
-100 |
|
2 |
0 |
Undefined |
|
2.1 |
0.1 |
10 |
|
2.01 |
0.01 |
100 |
|
2.5 |
0.5 |
2 |
|
3 |
1 |
1 |
|
4 |
2 |
½ |
|
5 |
3 |
1/3 |
|
6 |
4 |
¼ |
Note values of x taken near
asymptotes:
x
= 1.9, 1.99, 2.1, 2.01
b) For the domain, the graph extends indefinitely to the left and right but does not exist at x = 2. Therefore
For the range, the graph extends indefinitely up and down but does not exist at y = 0. Therefore
c) For the equation of the inverse, interchange x and y and then isolate y.
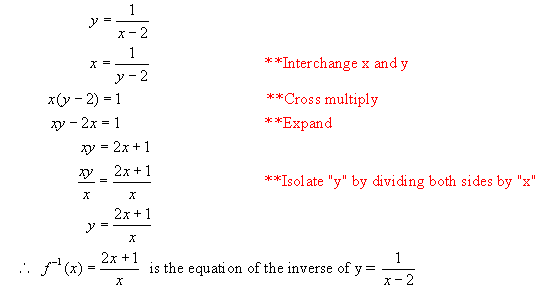
3. Sketch the graph of the reciprocal function for each of the following.
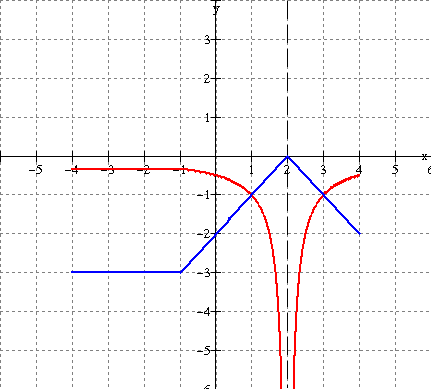
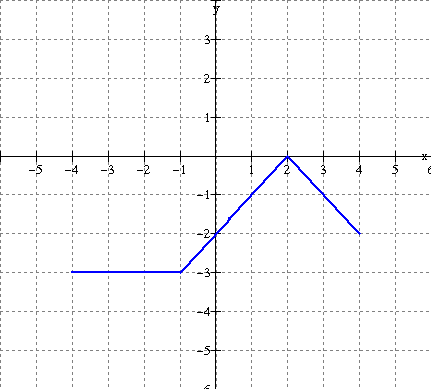
a)
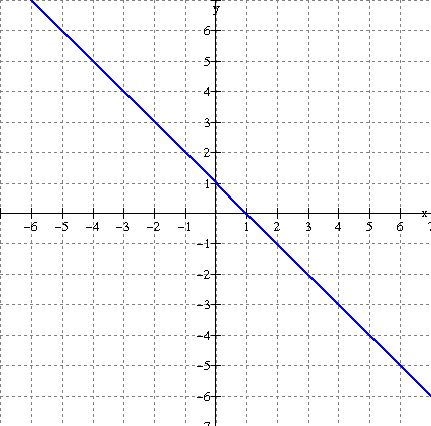
Solution:
The zero of f(x) is x = 1.
This is the vertical asymptote of the reciprocal.
Take
points on the graph of f(x) and use the mapping below.
(-3, 4) ----------------------------à (-3, ¼ )
(-1, 2) ----------------------------à (-1, ½ )
(0, 1) ----------------------------à (0, 1)
(1, 0) ----------------------------à V. Asymp.
(2, -1) ---------------------------à (2, -1)
(5, -4) ----------------------------à (5, -¼ )
See
graph below (red).
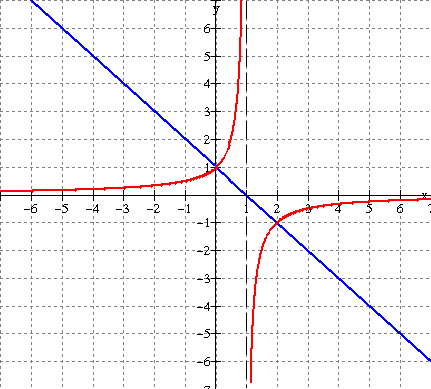
b)
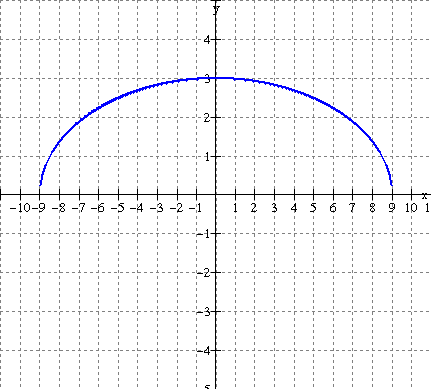Solution:
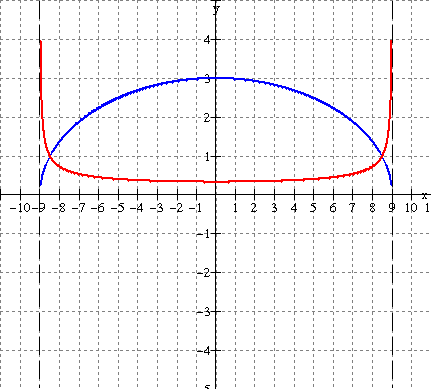
The zeros of f(x) are x = - 9 and x = 9. These are the vertical asymptotes of the
reciprocal.
Take points on the graph of f(x) and use the mapping below.
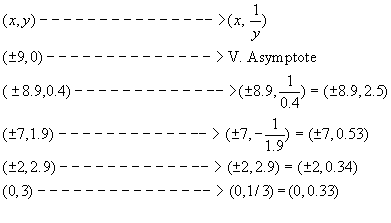
See graph below (red). Note that where f(x) = 1, the reciprocal function (red) equals 1
– ie – they meet where y = 1 on the graph 
c)
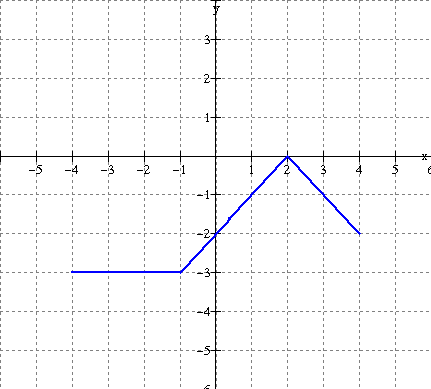
Solution:
The zero of f(x) is x = 2.
This is the vertical asymptote of the reciprocal.
Take
points on the graph of f(x) and use the mapping below.
(-4, -3)
----------------------------à
(-4, -1/3 )
(-1, -3) ----------------------------à (-1, -1/3 )
(0, -2)
-----------------------------à
(0, -½ )
(1, -1)
-----------------------------à
(1,-1)
(1.5, -½ )
--------------------------à (1.5, -2)
(2, 0)
------------------------------à V.
Asymp.
(2.5, -½ ) --------------------------à (2.5, -2)
(3, -1)
-----------------------------à
(3, -1)
(4, -2)
-----------------------------à
(4, -½ )
See
graph below (red).
