|
|
|
|
|
||||||||||
|
|
||||||||||||||

UNIT 2 : QUADRATIC FUNCTIONS & EQUATIONS
LESSON
6: COMPLEX NUMBERS DEFINED AS NON REAL
ROOTS OF QUADRATIC EQUATIONS
Recall the
properties of radicals:
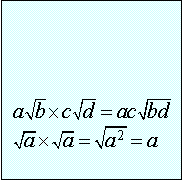
Solving
Quadratic Equations with Non-Real Roots:
Example 1: Solve the quadratic equation:
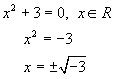
Previously
we would say this equation has no real
roots because of the
negative sign under the square root sign.
Definition:
![]()
We could
now write the roots as follows:

These
creatures with the i factor are called imaginary numbers. We use them when
solving quadratic equations with non real roots.
Example 2: Solve 4x2 – 2x + 3 = 0
Solution:
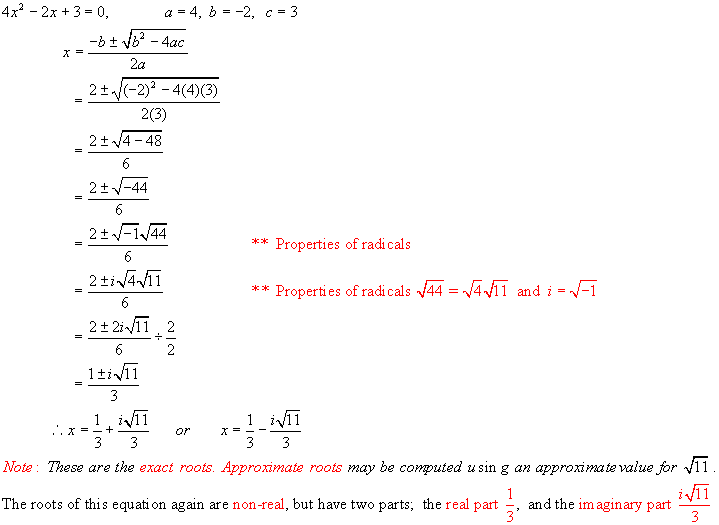
The
roots of this equation are examples of Complex
Numbers.
Note
that complex roots always occur in pairs called complex conjugates.
The Complex Number system is the union of the set of all Real Numbers with the set
of all Imaginary numbers (contain “i” factor)
It is
defined formally as follows:
![]()
![]()
Example 3: Solve 3x2
– 4x + 10 = 0 where x is a complex
number. Round roots to nearest
hundredth.
Solution:
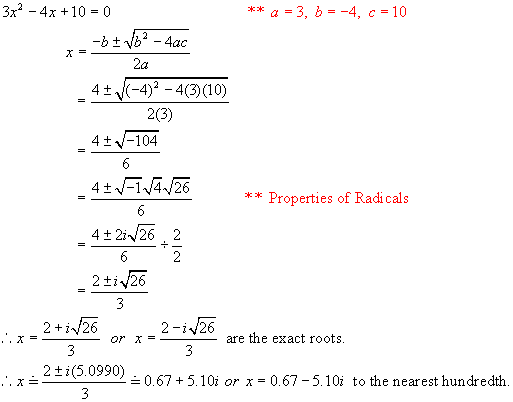
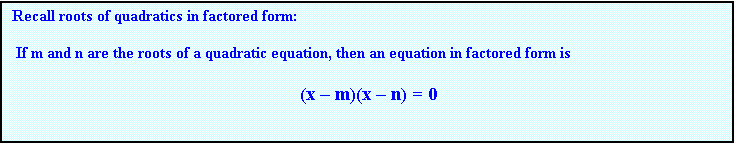
Example 3: Find a quadratic equation in factored form whose roots are
–4, 3
Solution:
(x - (-4))(x – 3) = 0
(x + 4)(x – 3) = 0
Example 4: Find a quadratic equation in factored form if one root is 2
+ 3i
Solution:
Since
complex numbers occur in conjugate pairs, the other root is 2 – 3i. Hence the equation is
[x - (2 + 3i)][x – (2 –
3i)] = 0 or
(x – 2 – 3i)(x – 2 +
3i) = 0