|
|
|
|
|
||||||||||
|
|
||||||||||||||

UNIT 3 : QUADRATIC FUNCTIONS & EQUATIONS
LESSON
9: REVIEW OF UNIT 3
Finding
Maximum or Minimum Values of Quadratic Functions:
Example:
Write y
= -3x2 15x 13 in vertex form y
= a(x h)2 + k
Solution:
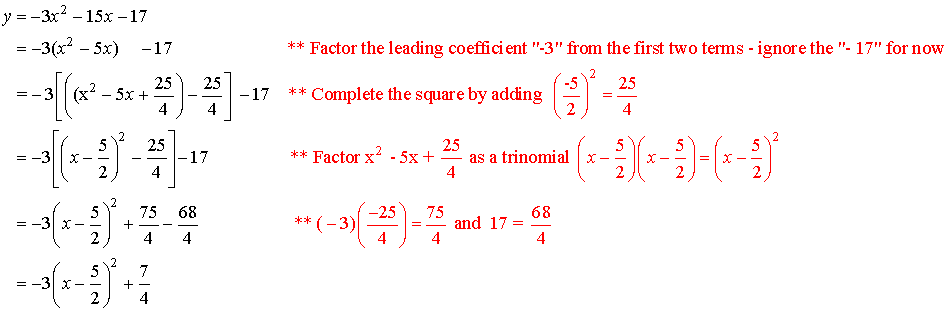
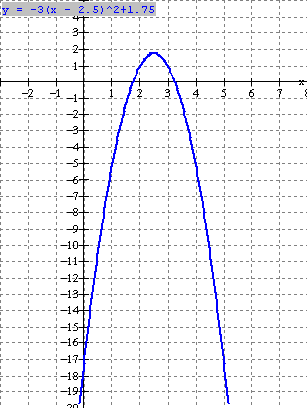 Because a < 0, the graph is a parabola which opens down
and has vertex at
Because a < 0, the graph is a parabola which opens down
and has vertex at 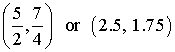 .
.
Since the parabola opens down, it will have a maximum value at
the vertex.
The maximum value is
![]() . See graph at left.
. See graph at left.
Quadratic
Equations:
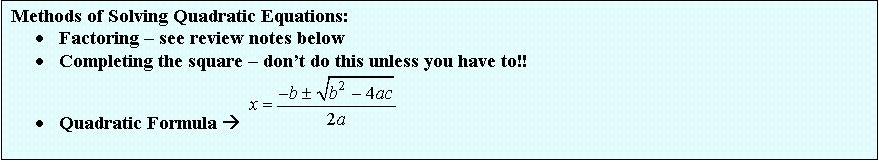
Review of Basic Factoring methods:
1. Common Factoring:
Factor 6x3 15x
Solution: 6x3 15x = 3x(2x2 5) **
Find the HIGHEST COMMON FACTOR for each term --- 3x
**
Divide 3x into each term to get the second factor --- 2x2 5
**
Check by expanding
2. Difference of Squares: Formula -- a2 b2 = (a b)(a + b)
Factor 49x2 64y2
Solution: 49x2 64y2 = (7x 8y)(7x + 8y)
Factor x2 9y2
Solution: x2 9y2 = (x 3y)(x + 3y)
3. Simple Trinomials: Form x2 + bx + c [Coefficient of x2 is 1]
a) Factor x2 + 5x + 6
Solution: Recall x2 + 5x + 6 = (x + __ )(x + __ ) **
We need two numbers that multiply to +6 and add to +5
** Check all pairs of factors of 6: {1, 6} adds to 7
{2, 3} adds to 5
Hence
x2 + 5x + 6 = (x + 3 )(x + 2) ** Check by expanding
4. Hard Trinomials: Form ax2 + bx + c [Coefficient of x2 does not equal 1]
a) Factor 6m2 5m 4
Solution:
We use the method of decomposition (although there are other methods)
We decompose the middle term -5m into two parts using the two clues:
Multiply
to (6)(-4) = -24 and
Add to -5
Strategy: List all pairs of factors of -24 and find the pair that adds to -5
** {1, 24} cannot obtain -5 with these two factors; 1+24=25; 1-24= -23
** {2, 12} cannot
obtain -5 with these two factors
** {3, 8}
-8 + 3 = -24 Choose these two
factors
Hence 6m2
5m 4 = 6m2 8m + 3m 4 ** -5m broken into two parts -8m + 3m
= 2m(3m 4) + 1(3m 4) ** Group by twos and common factor
= (3m 4)(2m + 1) ** check by expanding
Zeros
[x-intercepts]of Quadratic Functions:
Example 1:
Find the
zeros (x-intercepts) of the quadratic function f(x)
= 2x2 + x 6.
Solution:
We are
trying to find the points where the graph of the function crosses the x-axis
ie the x-intercepts.
Let y =
f(x) = 0 yielding the quadratic equation
2x2 + x 6 = 0. We
solve by factoring.
2x2 + x 6 = 0
2x2 + 4x 3x 6 = 0 ** See #4 above Hard Trinomials method
of decomposition
2x(x + 2) 3(x + 2) = 0 ** Common factor by grouping first two
terms and last two terms
(x + 2)(2x 3) = 0 ** Common factor (x + 2)
Hence
either x + 2 = 0 or 2x 3 = 0
and
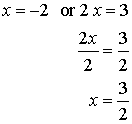
Therefore
the zeros are 2 and 3/2.
Note: Finding
zeros of a quadratic function always yields a quadratic equation to solve.
Example:
Solve 3x2
7x + 1 = 0 by completing the square.
Solution:
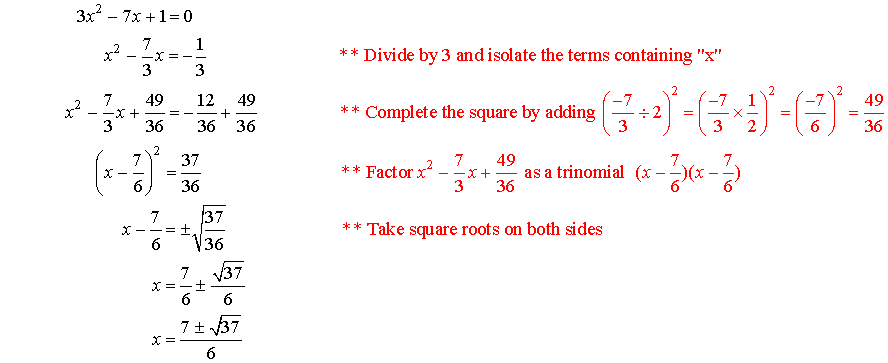
Example:
Solve 3x2
+ 6x + 1 = 0 using the quadratic formula.
Express roots to the nearest hundredth
Solution:
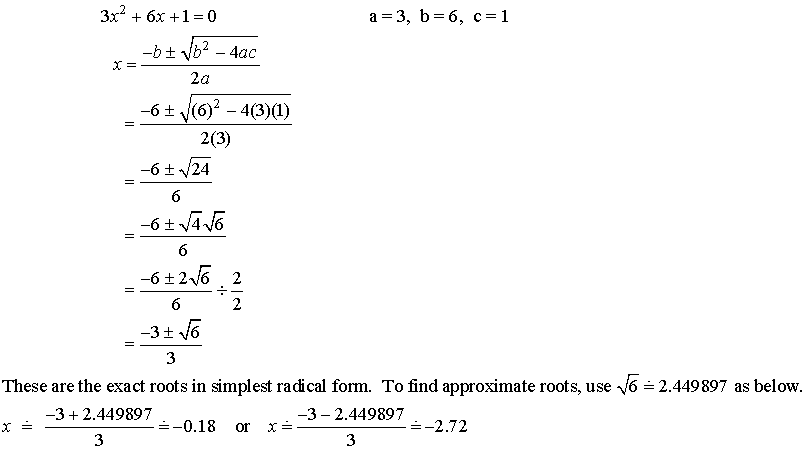
Finding
the number of roots of a Quadratic Equation :
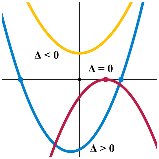
![Text Box: Method: use the Discriminant b2 4ac
· If b2 4ac > 0 then the equation has 2 real, distinct roots and the corresponding quadratic function will have two zeros or x-intercepts. The parabola will cut the x-axis in two distinct points
· If b2 4ac = 0 the roots are real and equal [1 real root]. The corresponding quadratic function will have one zero or x-intercept. The parabola will be tangent to the x-axis.
· If b2 4ac < 0 there are no real roots [or 2 imaginary roots]. The corresponding quadratic function will have no zeros or x-intercepts. The parabola is above or below the x-axis.
· See graphs below to illustrate these cases.](./quadrev_files/image020.gif)
|
Two zeros: b2
4ac > 0 |
One zero: b2 4ac = 0 |
No zeros: b2 4ac < 0 |
|
|
|
|
|
Here b2
4ac > 0 and the graph of the quadratic
function cuts the x-axis in 2 distinct points. The
quadratic equation has 2 real, distinct
roots. |
Here b2
4ac = 0 and the graph of the
quadratic function is tangent to the x-axis yielding 1 x-intercept. The
quadratic equation has 2 real, equal
roots. Some texts say 1 real
root for this case. |
Here b2
4ac < 0 and the graph of the
quadratic function does not cut the x-axis.
The
quadratic equation has no real roots or
imaginary roots. |
Example:
In each case,
calculate the value of the discriminant b2 4ac and determine the
number of zeros of the quadratic function.
a) f(x) = 2x2 + 3x 1 b) g(x) = 16 x2 c) y = 3x2 2x + 5 d) y = x2 6x + 9
Solutions:
a = 2 b = 3 c= -1
a) f(x) = 2x2 + 3x 1
b2 4ac = (3)2
4(2)(-1)
= 9 + 8
= 17
Since b2
4ac > 0, there are 2 zeros.
The corresponding quadratic equation
2x2 + 3x 1 = 0 has 2
real distinct roots.
a = 3 b = -2 c = 5
c) y = 3x2 2x + 5
b2
4ac = (-2)2 4(3)(5)
= 4 60
= -56
Since b2
4ac < 0, there are no zeros.
The corresponding quadratic equation
3x2 2x + 5 = 0 has no real roots.
a = 1 b = -6 c = 9
d) y = x2 6x + 9
b2 4ac = (-6)2
4(1)(9)
= 36 36
= 0
Since b2 4ac = 0, there is 1 zero. The corresponding quadratic equation x2 6x + 9 = 0 has 1 real root or real and equal roots.
Example:
In each case, determine the number x-intercepts of the quadratic function.
Solutions:
a) f(x) = 5x2 3x + 2
a = 5 b = -3 c = 2
b2 4ac = (-3)2
4(5)(2)
= 9 40
= -31
Since b2 4ac < 0, there are no x-intercepts or zeros. The corresponding quadratic equation 5x2 3x + 2 = 0 has no real roots
Example:
For what
value of k does the equation kx2
4x + 2 = 0 have:
a)
exactly one root [real equal roots] ?
b) 2
real distinct roots ?
Solutions:
a = k b = -4 c = 2
a) For 1
real root set b2 4ac = 0
(-4)2 4(k)(2) = 0
16 8k = 0
- 8k =
-16
k =
2
b) For 2
real distinct roots set b2 4ac > 0
(-4)2 4(k)(2)
> 0
6 8k > 0
- 8k > -16
k <
2 ** The inequality reverses when dividing
by a negative
2. Quadratic Function Problems (Max/Min
Problems)

Area
Problems:
Example:
Farmer
Al has 240 m of fencing available. He
wishes to enclose a rectangular garden with this fence. One side borders a stream bank and requires
no fence. Find the dimensions he should
use to enclose a field of maximum area.
Solution:
ΰ Determine
what is unknown or what you are asked to find?
Assign variables to the unknowns. Here the
dimensions of the field are unknown.
Let the length be x and the width be y.
Stream bank
y y
x
ΰ Determine the quantity to be
maximized or minimized.
We are asked to maximize the area. Hence our formula is:
![]() ** This is your main function for the problem
** This is your main function for the problem
ΰ
Write
this formula as a function of one variable. Since
the available fencing is240 m, we have a secondary relation between the two
variables.

3. Quadratic Equation Problems
Example:
A farmer
has 80 m of fencing available. He
wishes to enclose a rectangular field of area 300 m2. Find the dimensions of the field.
x
y
Solution:
ΰ Determine
what is unknown ? Assign variables to
the unknowns. Here we are asked to find the width and
length of the field.
Let the
length of the field be x and the width be y.
ΰ
We are told the area is 300 m2. Write this statement as an equation.
![]()
ΰ
Write
this as an equation in one variable. Since the perimeter is 80, we have
a secondary relation between the two variables.
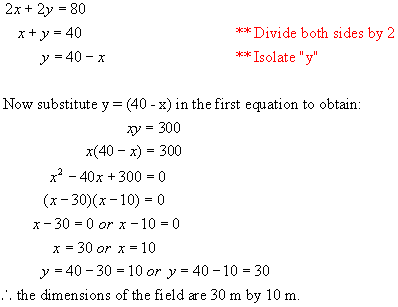
![Text Box: Strategies for Solving Quadratic Equations Problems.
· Determine what is unknown or what you are asked to find. Draw a diagram if possible.
· Assign variables to these unknowns. You can use a single variable as in examples 3 & 4 or use two variables as in examples 1 & 2. These are your let statements.
· Translate the information in the problem into an algebraic equation.
· Write this as an equation in one variable if needed [ see examples 1 & 2 ].
· Put all the terms on one side of the equation and solve by factoring or the quadratic formula.](./quadrev_files/image036.gif)
Properties
of Radicals:
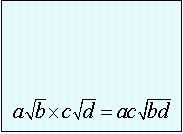
Example:
Write as mixed radicals.
![]()
![]()
Solutions:
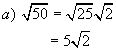
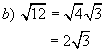
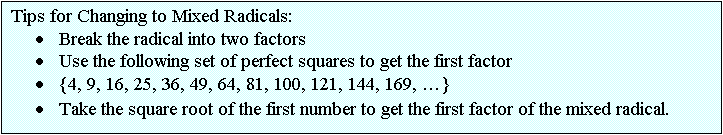
Example:

Example:
Simplify
![]()
![]()
![]()
![]()
Solutions:
Again we
follow the rules of ordinary algebra for expanding
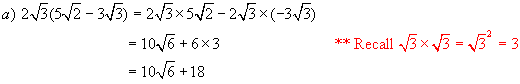
![]()
Recall
from ordinary algebra the product of two binomials:
(x + 3)(x + 5) = x(x + 5) + 3(x + 5)
= x2 + 5x + 3x + 15
= x2
+ 8x + 15
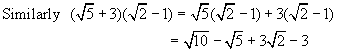
Example 8:
Simplify by rationalizing the
denominator.
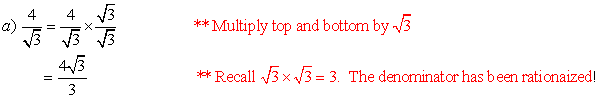
Example 10: Simplify

Solving
Quadratic Equations with Non-Real Roots:
Example 3: Solve 3x2
4x + 10 = 0 where x is a complex
number. Round roots to nearest
hundredth.
Solution:
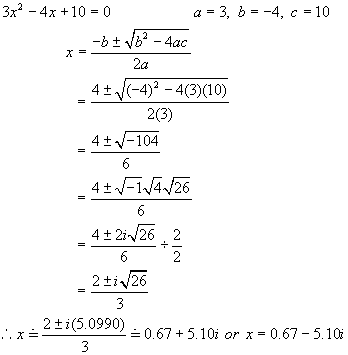
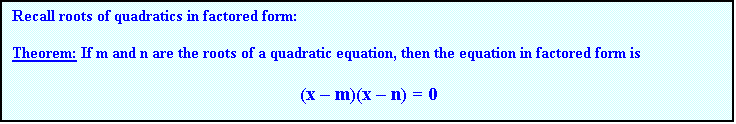
Example 3: Find the quadratic equation in factored form whose roots
are 4, 3
Solution:
(x - (-4))(x 3) = 0
(x + 4)(x 3) = 0
Example 4: Find the quadratic equation in factored form if one root is
2 + 3i
Solution:
Since
complex numbers occur in conjugate pairs, the other root is 2 3i. Hence the equation is
[x - (2 + 3i)][x (2
3i)] = 0 or
(x 2 3i)(x 2 + 3i) = 0
Operations
with Complex Numbers:
Example 2:
![]()
![]()
![]()
Solutions:

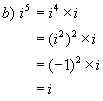

Complex
Conjugates:
Complex
conjugates are often denoted using the notation ![]() .
.
Example 3:
![]()
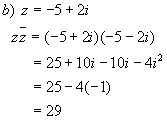
Note that in all cases the product of a complex number and its conjugate is a real number.
Graphing
functions and their reciprocals:
Example 1:
![]()
|
x |
|
|
|
-4 |
- 6 |
-1/6 |
|
-2 |
- 4 |
- Ό |
|
-1 |
- 3 |
-1/3 |
|
0 |
-2 |
-½ |
|
1 |
-1 |
-1 |
|
1.5 |
-0.5 |
-2 |
|
1.75 |
-0.25 |
-4 |
|
2 |
0 |
1/0 = undefined |
|
2.25 |
0.25 |
4 |
|
2.5 |
0.5 |
2 |
|
3 |
1 |
1 |
|
4 |
2 |
½ |
|
5 |
3 |
1/3 |
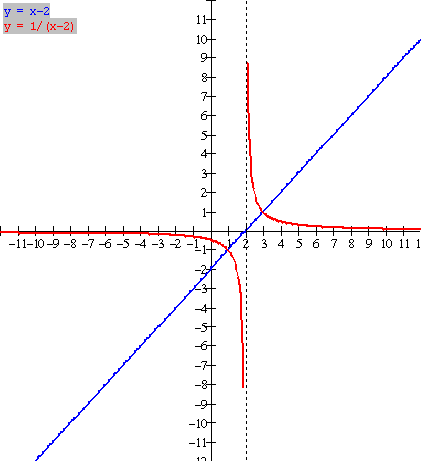
Please note the following from the graph and table:
·
The
graph of y = f(x) = x 2 (blue) is a line and its reciprocal (red) has 2 branches separated by the line x = 2 (dashed). It is called a
hyperbola.
·
Where
f(x) has a zero (x intercept), the reciprocal has
an asymptote (x = 2 dashed)
·
The
behaviour near the asymptote is interesting;
as x approaches 2 from the right (x = 3, 2.5, 2.25
), the reciprocal (red) gets very large in the positive direction; as x approaches 2 from the left (x = 1, 1.5,
1.75
), the reciprocal (red) gets very large in the negative
direction.
·
As x
takes on larger positive values, the reciprocal takes on smaller values
approaching zero from above. As x takes
on larger negative values
(-1,-2, -4, -10,
), the reciprocal takes on smaller values approaching
zero again from below.
·
Where
f(x) is positive, the reciprocal is positive;
where f(x) is negative, the reciprocal is negative.
·
Where
f(x) = 1, the reciprocal equals 1; where
f(x) = -1, the reciprocal equals 1.

Example 3:
![]()
Solution:
First
find the zeros or x intercepts. Let y
= 0 and solve for x.
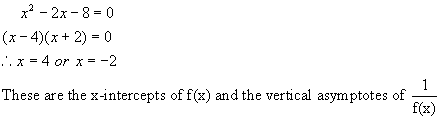
Next
find the vertex.
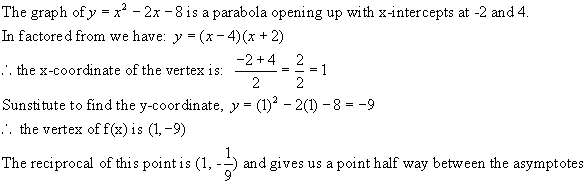
Now make
a table of values as above including points near the asymptotes x = -2 and x =
4
|
x |
|
|
|
-4 |
12 |
1/12 |
|
-3 |
7 |
1/7 |
|
-2.5 |
3.25 |
0.31 |
|
-2.1 |
0.61 |
1.64 |
|
-2.01 |
0.0601 |
16.64 |
|
-2 |
0 |
Undef. |
|
-1.99 |
-0.0599 |
-16.69 |
|
-1.9 |
-0.59 |
-1.69 |
|
1 |
-9 |
-1/9 |
|
3.9 |
-0.59 |
-1.69 |
|
4 |
0 |
Undef |
|
4.1 |
0.61 |
1.64 |
|
5 |
7 |
1/7 |
|
6 |
12 |
1/12 |
Note values of x taken near asymptotes:
x
= - 2.1, -2.01, - 1.9, -1.99, 3.9, 4.1
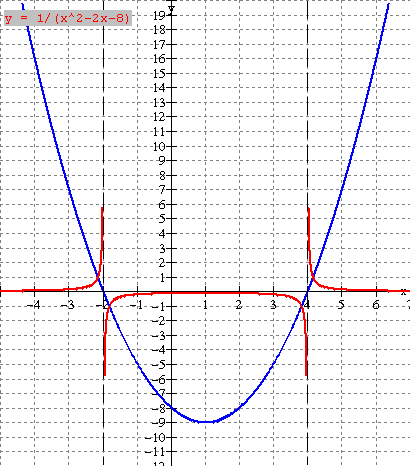
Please note the following from the graph and table:
·
The graph
of y = f(x) = x2 2x - 8 (blue) is a parabola with vertex at (1, -9) and zeros 2, 4. Its reciprocal (red) has 3 branches separated by the lines
x = - 2 and x
= 4(dashed).
·
Where
f(x) has a zero (x intercept), the reciprocal has
an asymptote (x = - 2 and x = 4 dashed)
·
The
behaviour near the asymptotes is interesting;
as x approaches - 2 from the right (x = -1.9, -1.99 in table), the
reciprocal (red) gets very large in the negative
direction (goes down); as x approaches
- 2 from the left (x = - 2.1, -2.01 in table), the reciprocal (red) gets very large in the positive direction (goes up). Similar behaviour occurs near the other
asymptote x = 4.
·
As x
takes on larger positive values (x = 5, 6 in table), the reciprocal takes on
smaller values approaching zero from above.
As x takes on larger negative values (- 3, - 4 in table), the reciprocal
takes on smaller values approaching zero again from above.
·
Where
f(x) is positive, the reciprocal is positive; where f(x) is negative, the reciprocal is
negative.
·
Where
f(x) = 1, the reciprocal equals 1;
where f(x) = -1, the reciprocal equals 1.