New Topic

Exponents

Exponential Equations I

Exponential Functions

The Exponential Function Base e

The Logarithm Function

Logarithmic & Exponential Equations

Applications:Growth & Decay

Review&Test

UNIT 5 : EXPONENTIAL & LOGARITHMIC FUNCTIONS

LESSON 8: LOGARITHMIC EQUATIONS SUMMARY AND REVIEW

LESSON 1: LAWS OF EXPONENTS

Examples of Powers:

2⁵ = 2 x 2 x 2 x 2 x 2 = 32; (-3)³ = (-3) x (-3) x (-3) = -27; 2.7² = 2.7 x 2.7 = 7.29

A POWER (a^m ) consists of two parts; the base “a” and the exponent “m”.

Review of Basic Exponent Laws:

Rule	Example	Explanation
a^m x a^n = a^m+n	3^2 x 3^5 = 3^7	Multiplication Rule - If the bases are the same, add the exponents
		Division Rule - If the bases are the same, subtract the exponents
(a^m)^n= a^mn	(3^2)^3=3^6	Power Rule – When taking a power of a power, multiply the exponents
(ab)^m= a^ma^m	(3 x 2)^4 = 3^4 x 2^4	Power of a Product – Take each factor in the product to that power
		Power of a Quotient – Take numerator and denominator to that power

Zero Exponents: Rule: a⁰ = 1

Examples : 2⁰ = 1; (-3.4)⁰ = 1 (x²)⁰ = 1; Note that 0⁰ is not defined.

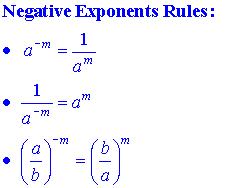
Examples :

Example : Simplify

Solutions:

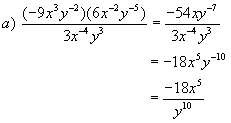
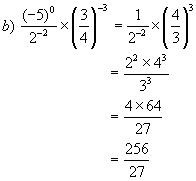
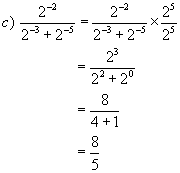
Rational Exponents:

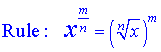
Examples :

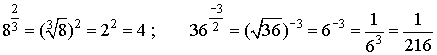
LESSON 2: Exponential Equations: 2^x = 64; 9^{2x – 1} = 729; 500(1.02)^{x – 1} = 897.56

Theorem: If a^x = a^y, then x = y. In words: If an exponential equation has the bases equal, then the exponents must be equal.

This theorem gives us our strategy for solving exponential equations, namely convert each side of the equation to a common base.

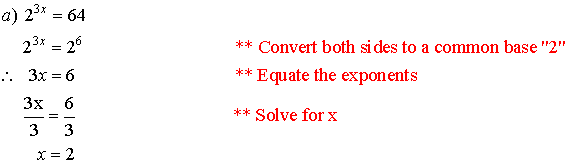
Growth and Decay problems:

Example:

The half-life of radium is 1600 years. What fraction of radium remains from a sample after 12 800 years?

Solution: Again let the starting mass be 1 g.

Recall:

A = ?

A₀ = 1 g

t = 12 800 years

h = 1 600 years

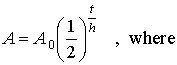
· A is the mass remaining after the decay period

· A₀ is the original mass of radioactive material

· ½ is the decay factor

· t is the total time elapsed

· h is the half-life of the material

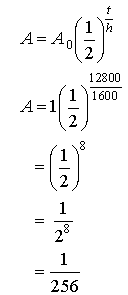
Example:

A bacteria culture doubles in size every 20 min. How long will it take for a sample of 10 bacteria to grow to 20 480?

Solution:

A = 20 480

A₀ = 10

t = ?

d = 20 min.

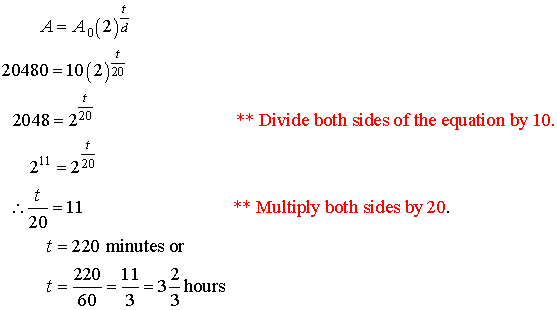
Therefore it will take 3 2/3 hours.

LESSON 3: Exponential Functions:

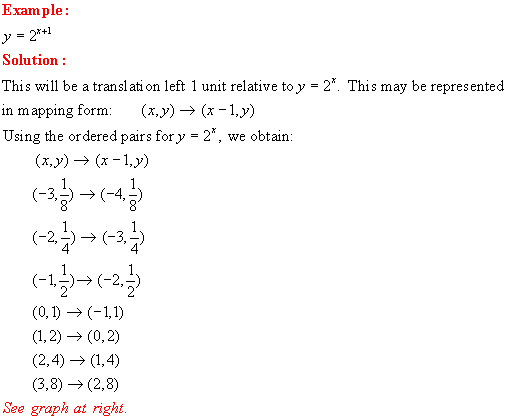
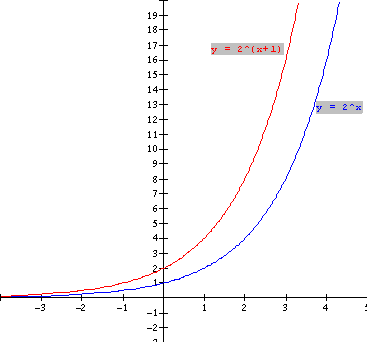
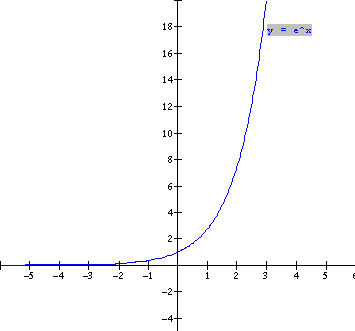
LESSON 4: THE EXPONENTIAL FUNCTION y = e^x

Table of Values & graph:

x
-3
-2
-1
0	1
1
2
3
4

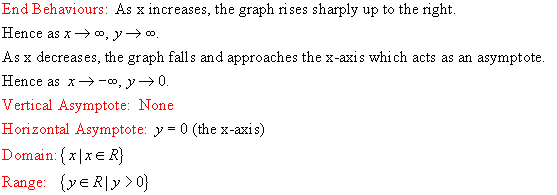
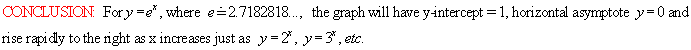
LESSON 5: The Logarithmic Functions:

Logarithmic functions are the inverses of exponential functions.

Table of Values & Graphs:

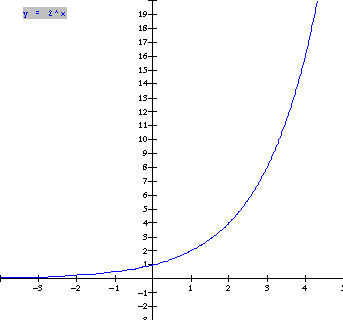
x	y
-3
-2
-1
0	1
1
2
3	8
4	16

Now form the inverse of this function by interchanging x and y in the ordered pairs and the equation.

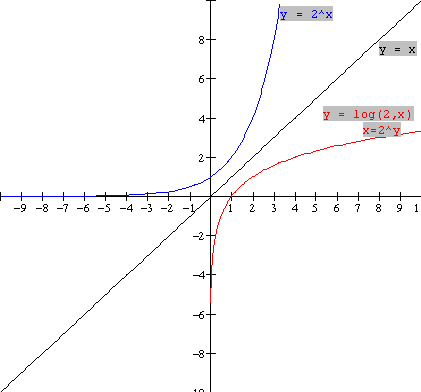
x	y
	-3
	-2
	-1
1	0
	1
	2
8	3
16	4

The equation of the inverse is found by interchanging x and y in the equation y = 2^x. This yields x = 2^y. If we put this equation in logarithmic notation,

we obtain the logarithmic function y = log₂x. The graph is a reflection in the line y = x of the exponential function y = 2^x and is shown in red above.

The Natural Logarithmic Function y = log_ex or y = ln x:

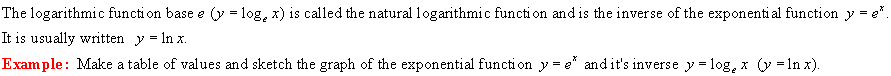
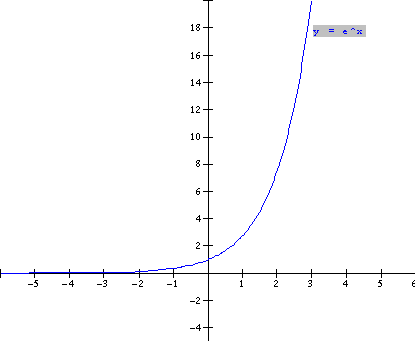
x
-3
-2
-1
0	1
1
2
3
4

Now form the inverse – interchange the components of the ordered pairs:

x	y
	-3
	-2
	-1
1	0
	1
	2
	5
	4

The equation of the inverse is found by interchanging x and y in the equation y = e^x. This yields x = e^y.

If we put this equation in logarithmic notation, we obtain the logarithmic function y = log_ex or y = lnx.

The graph is a reflection in the line y = x of the exponential function y = e^x and is shown in red above.

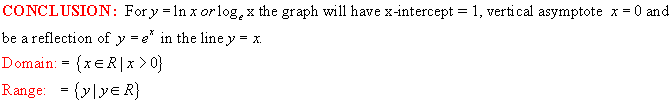
Logarithms:

Note: When we read log₂8, we ask the question “To what exponent must base 2 be raised to give 8?” The answer is of course 3

and this idea gives rise to the following definition.

Definition: the expression log_ax is defined to mean “ the exponent to which base a must be raised to give x.

The expression reads: “ the logarithm of x, base a.”

Hence log₁₀100 means the exponent to which base 10 must be raised to give 100. The answer is 2, giving the statement log₁₀100 = 2.

Hence log₃81 means the exponent to which base 3 must be raised to give 81. The answer is 4, giving the statement log₃81 = 4.

Exponential Form	Logarithmic Form
3^4 = 81	log381 = 4
5^2 = 25	log525 = 2
2^5 = 32	log232 = 5
10^3 = 1000	log101000 = 3

The following properties of logarithms are important and used frequently in our study of logarithms. They correspond closely to

our rules for exponents studied earlier.

The following properties of natural logarithms are important and used frequently in our study of logarithms.

They correspond closely to our previous rules for logarithms studied above.

LESSON 6: LOGARITHMIC EQUATIONS

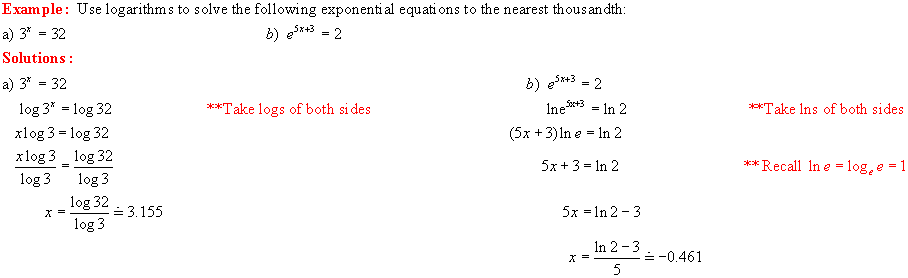
LESSON 7: Growth and Decay Problems Revisited:

Growth and decay problems are governed by the following formula:

Return to top of page

Click here to go to Chapter Test