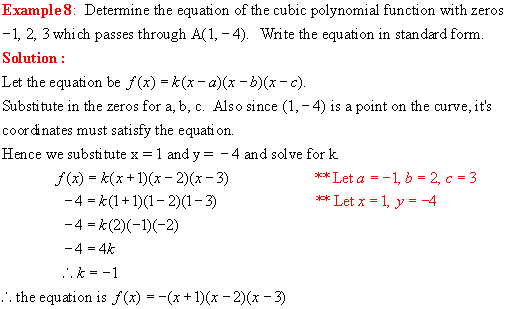jdlogo

UNIT 4 : POLYNOMIAL AND RATIONAL FUNCTIONS

LESSON 1: POLYNOMIAL FUNCTIONS INTRODUCTION

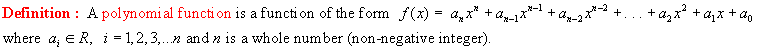
Example 1:

f(x) = x³ – 4x² + x + 6 is a cubic polynomial function because the largest exponent of the variable is 3. Make a table of values or use

a graphing calculator to draw it’s graph [see below].

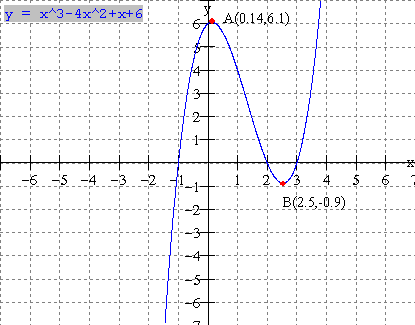Note: The function has 3 zeros (x – intercepts), x = -1, 2, 3 and two

turning points A and B. Turning point A is a local maximum point as

the function changes from increasing to decreasing at A. Turning point B

is a local minimum point as the function changes from decreasing to increasing

at B. The function has a local maximum value of y = 6.1 at point A and a

local minimum value of y = -0.9 at point B.

Text Box: In general a cubic function will have at most 3 zeros and at most 2 turning points. There could be fewer. (see example 2 below).
A quartic function (degree 4) will have at most 4 zeros and 3 turning points. Again there could be fewer. (see example 3 below).

Example 2:

Use your graphing calculator to graph and study the cubic functions below.

a) f(x) = – x³ – x² + 5x – 3 b) f(x) = (x – 3)³ + 1

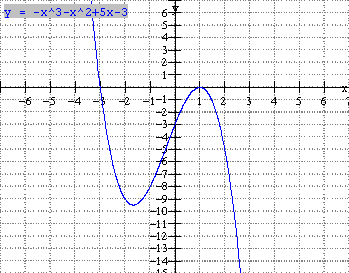
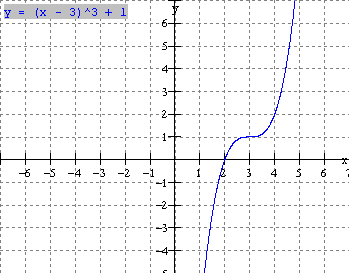
c) f(x) = x³ + 3x² + 3x + 2

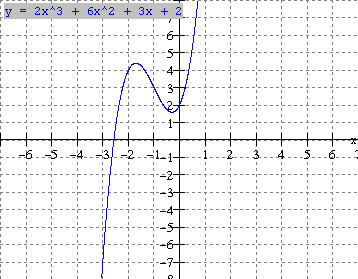
Note: From the examples above we can make the following observations.

A cubic function can have 1, 2 or 3 zeros (x-intercepts)
It can have 0 or 2 turning points.
The coefficient of x³ is called the leading coefficient (k). In (a) the leading coefficient is negative(k = -1) and the function rises to the left and falls to the right.

The leading coefficient(k) determines the end behaviours. If k > 0, the function falls to the left and rises to the right (ex. 1, 2 b,c)

If k < 0, the function rises to the left and falls to the right (ex. 2a). This characteristic is true for all polynomial functions of odd degree (1, 3, 5, …).

Example 3:

Use your graphing calculator to graph and study the quartic functions below.

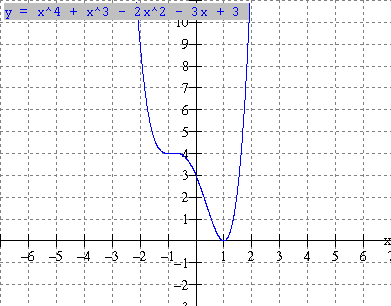
a) f(x) = x⁴ + x³ –5x² – 3x b) y = x⁴ + x³ – 2x² – 3x

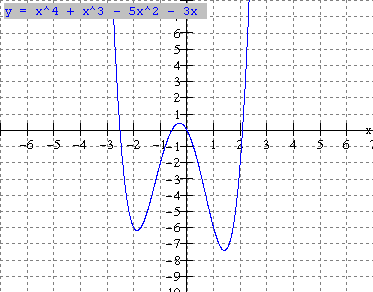
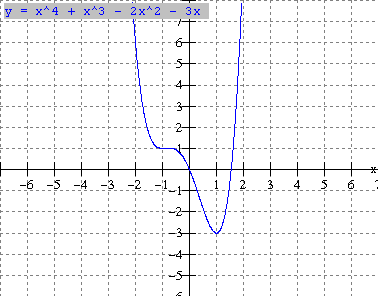
c) y = -0.5x⁴ – x³ + 2x² – 5 d) y = x⁴ + x³ – 2x² – 3x + 3

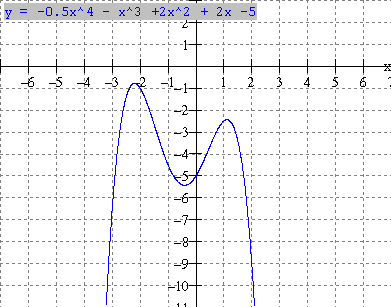
Note: From the examples above we can make the following observations.

A quaric function can have 0,1, 2, 3 or 4 zeros (x-intercepts)
It can have 1 or 3 turning points.
The coefficient of x⁴ is called the leading coefficient (k). In (c) the leading coefficient is negative(k = -0.5) and the function falls to the left and right.

In (a,b,d) the leading coefficient is positive and the function rises to the left and right

The leading coefficient(k) determines the end behaviours. If k > 0, the function rises to the left and right (ex. 3 a,b,d)

If k < 0, the function falls to the left and right (ex. 3c). This characteristic is true for all polynomial functions of even degree (2, 4, 6, …).

Polynomial Functions in Factored Form f(x) = k(x – a)(x – b)(x – c) . . . etc.

Linear Functions in factored Form: f(x) = k(x – a)

Text Box:

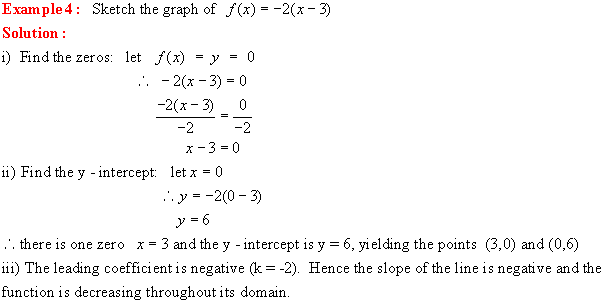
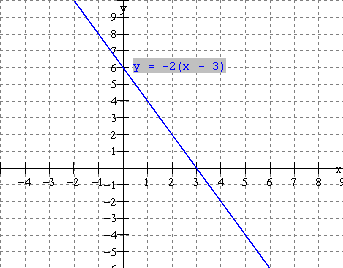
Quadratic Functions in factored Form: f(x) = k(x – a)(x – b)

Text Box:

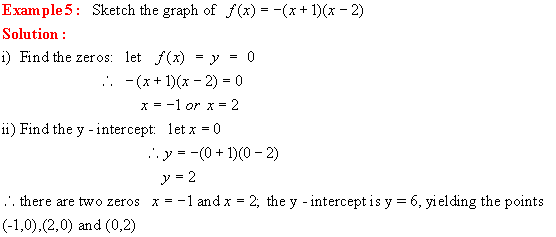
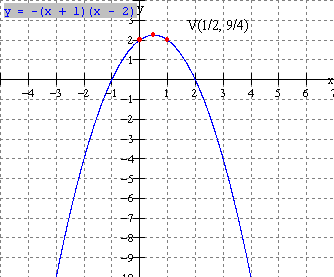
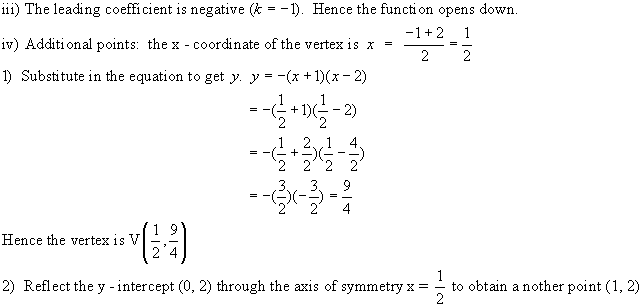
Cubic Functions in factored Form: f(x) = k(x – a)(x – b)(x – c)

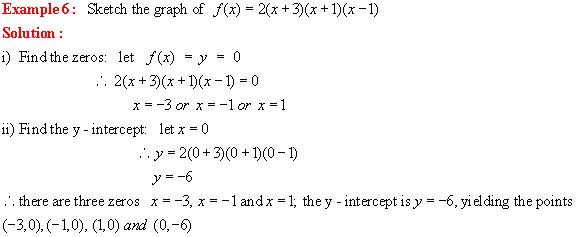
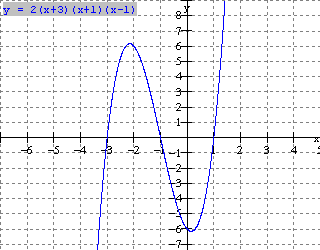
x	y
-2	6
0	-6

Text Box:

Quartic Functions in factored Form: f(x) = k(x – a)(x – b)(x – c)(x – d)

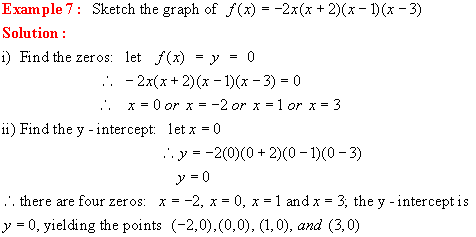
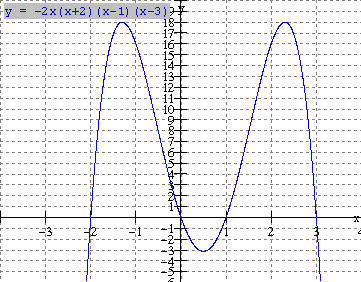
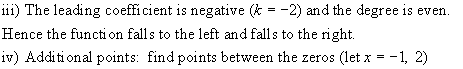
x	y
-1	16
2	16

Text Box:

Return to top of page

Click here to go to homework questions