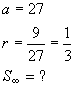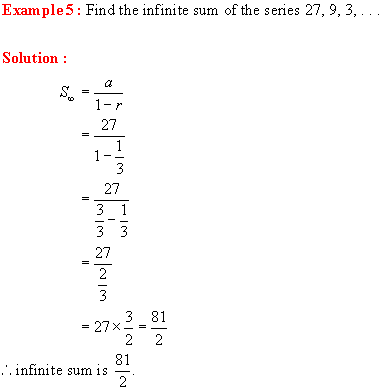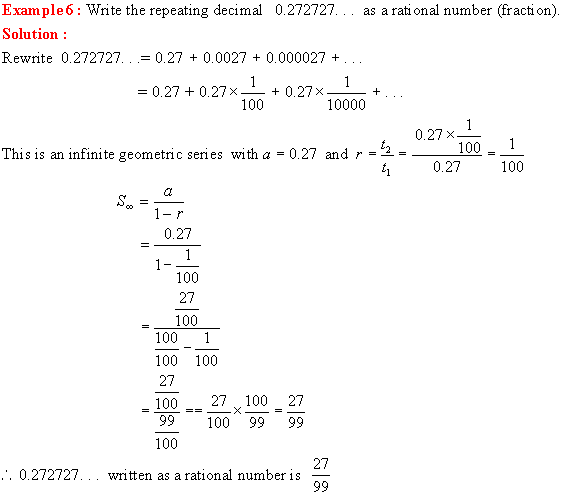|
|
|
|
|
||||||||
|
|
||||||||||||

UNIT
8 :
SEQUENCES AND SERIES
LESSON 4:
GEOMETRIC SERIES
Geometric
Series:
Recall a sequence such as 2, 4, 8, 16, 32, … is called a Geometric
Sequence. These sequences have the following properties.
·
Terms
are denoted as t1 , t2 , t3 , referring
to term1, term 2,
term 3 …
·
![]()
·
This
ratio is called the common ratio and denoted using the letter r. Here r = 2.
·
The
first term is denoted using the letter a. Here a = 2.
·
Successive
terms are found by multiplying a given term by the common ratio. Eg.
t6 = 32 x 2 = 64 etc.
·
The
formula for the general term or nth term is tn = arn-1.
·
Geometric
sequences are exponential functions with domain the natural numbers N
= {1, 2, 3, 4, …}
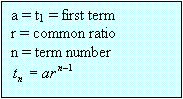
Definition: The sum of the terms of a
Geometric sequence is a Geometric Series.

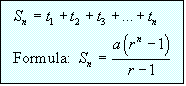
Example 1:
Form the
geometric sequence determined by the exponential function f(n) = 3(2)n-1. Find a, r and S10.
Solution:
a = 3 r = 2 n = 10 S10 = ?
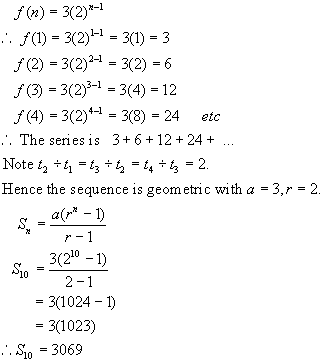
a = - 2 r = 3 n = 9 S9 = ?
Example 2: Given the first few
terms.
Given
the series –2 – 6 – 18 – 54 – …
a) Show
that the series is geometric.
b) Find
S9
Solution:

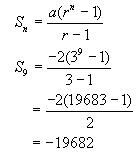
Example 3: Given the first
and last terms.
Given
the series 2 + 8 + 32 + … + 32768.
Find the sum of the series.
Solution: First find the number of terms n.
Let the
last term be tn.
a = 2 r = 4 n = ? tn = 32768 Sn = ?
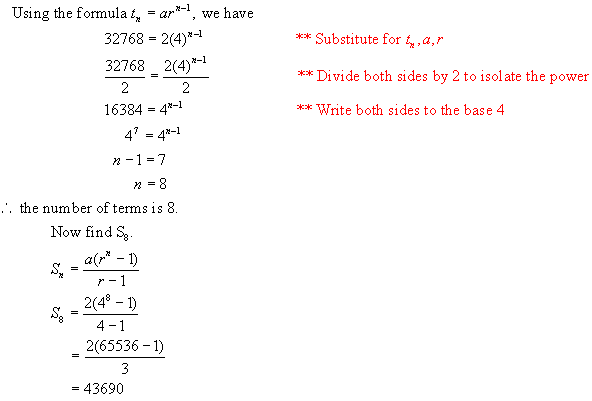
Example 4: When r is
negative or fractional.
a) Given
the geometric series –3 + 6 – 12 + 24 – …
Find a, r and S12.
Solution:
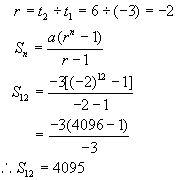
Infinite
Geometric Series: