|
|
|
|
|
||||||||
|
|
||||||||||||

UNIT
8 :
SEQUENCES AND SERIES
LESSON 7:
UNIT 8 SUMMARY
Arithmetic
Sequences:
A sequence
such as –2, 3, 8, 13, … is called an Arithmetic
Sequence. These sequences have the following
properties.
·
Terms
are denoted as t1 , t2 , t3 , referring
to term1, term 2,
term 3 …
·
The difference between successive terms is constant. ie t2
– t1 = t3 – t2 = t4 – t3
etc
·
This
difference is called the common
difference and denoted
using the letter d. Here d
= 5.
·
The
first term is denoted using the letter a. Here a = -2.
·
Successive
terms are found by adding the common difference, d, to the preceding
term. Hence t5 = 13 +
5 = 18 etc.
·
The
formula for the general term or nth term is tn = a + (n
– 1)d
·
Arithmetic
sequences are linear functions with domain the natural numbers N =
{1, 2, 3, 4, 5, …}

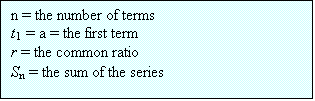
Arithmetic
Series:
Definition: The sum of the terms of an
arithmetic sequence is an Arithmetic Series.
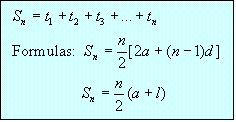

Example:
![]()
a = 255 d = -4 n = ? tn = 3 Sn = ?
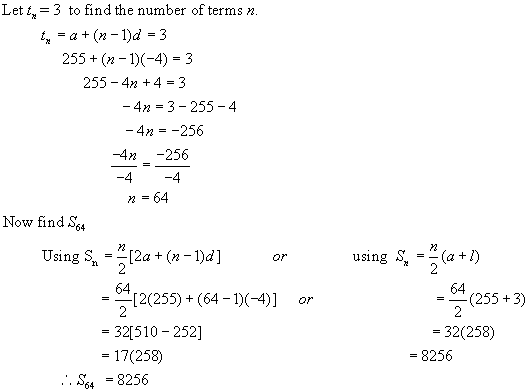
Geometric
Sequences:
A
sequence such as 2, 4, 8, 16, 32, … is called a Geometric Sequence. These sequences
have the following properties.
·
Terms
are denoted as t1 , t2 , t3 , referring
to term1, term 2,
term 3 …
·
The ratio of any term to the term preceding is constant.
![]()
·
This ratio
is called the common ratio and denoted using the letter r. Here r = 2.
·
The
first term is denoted using the letter a. Here a = 2.
·
Successive
terms are found by multiplying a given term by the common ratio. Eg.
t6 = 32 x 2 = 64 etc.
·
The formula
for the general term or nth term is
tn = arn-1.
·
Geometric
sequences are exponential functions with domain the natural numbers N
= {1, 2, 3, 4, 5 …}

Geometric
Series:
Definition: The sum of the terms of a
Geometric sequence is a Geometric Series.
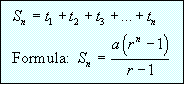
Example:
a = 4 r = 2 n = ? tn = 1024 Sn = ?
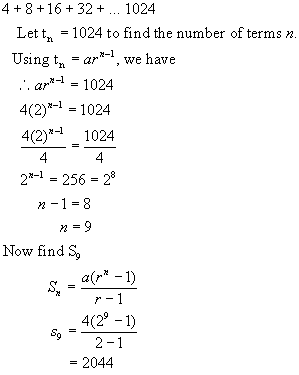
Sigma
Notation:
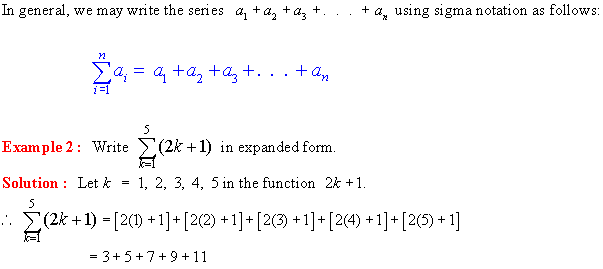
Mathematical
Induction:
Axiom
of Mathematical Induction:
If a
certain hypothesis is true for a finite set of natural numbers S, we need to show
that the set S equals N, the set of all natural numbers.
The
following axiom of induction will assist us in this quest.