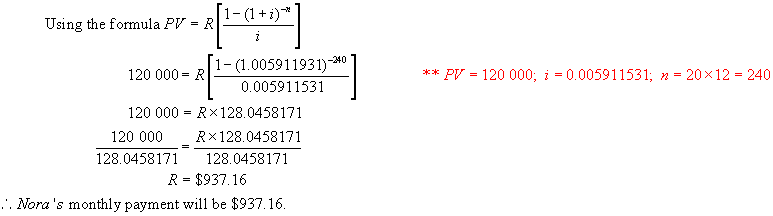|
|
|
|
|
||||||||
|
|
||||||||||||
|
|
UNIT
9 :
MATHEMATICS OF INVESTMENT
LESSON 6:
MORTGAGES HOMEWORK QUESTIONS
Homework Questions: (Solutions below)
1 a)
Greg and Beth are house hunting.
They have been pre-approved for a maximum mortgage of $180 000. If they use the full amount ($180 000), and will
repay it in monthly instalments over 35 years, find the monthly payment if the
interest rate is 7.2%/a, compounded semi-annually.
b) Determine the total interest paid over the
35 year period.
2. In the question above, determine the
outstanding balance at the end of 10 years.
3. The Sturrocks purchased a cottage on Little
Straggle Lake for $140 000. They paid
25% down, financing the rest with a mortgage over 20 years with interest at
7.8%/a, compounded semi-annually.
a) Determine the monthly payment.
b) Determine the total amount of interest paid.
4. In question 3 above, suppose the initial
term of the mortgage was 5 years at which time the terms are renegotiated.
a) Find the amount still owing at this time.
b) Determine the new monthly payment to
maintain the mortgage if the rate changes to 8.4%/a, compounded semi-annually.
5 a)
Nora has just purchased a new home. For $220 000. If she will pay $100 000 down and mortgage the
rest it in weekly instalments over 20 years, find the weekly payment if the
interest rate is 7.2%/a, compounded semi-annually.
b) If she had chosen monthly payments at the
same rate, what would the payment be?
1 a)
Greg and Beth are house hunting.
They have been pre-approved for a maximum mortgage of $180 000. If they use the full amount ($180 000), and
will repay it in monthly instalments over 35 years, find the monthly payment if
the interest rate is 7.2%/a, compounded semi-annually.
b)
Determine
the total interest paid over the 35 year period.
Solution:
Here the
payment interval (monthly ) is different than the interest period
(semi-annual). This is a general annuity.
We must
match the interest period to the payment interval.
Ie. We must
find the monthly rate that is equivalent to 7.2%/a, compounded semi-annually.
Step 1:
Using the formula A = P(1 + i)n,
find the value of $1 invested at 7.2%/a, compounded semi-annually after 1 year.
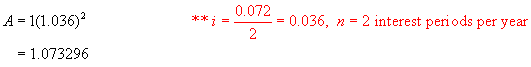
Step 2:
Let the equivalent monthly rate be i %. (Note the equivalent yearly rate would be 12i %.)
Now find the value of $1 invested at i % per month after 1 year.
A = 1(1 + i)12 ** n = 12, the number of times interest is
compounded per year.
Step 3:
These two amounts must be equal.
Hence
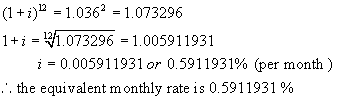
The money in question is borrowed now – at
point 0 on the time line. Hence this is
a PV general annuity question
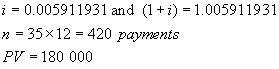
![]()
![]()
![]()
![]()
![]()
![]()
![]() Interest Period 0 1 2 3 418 419 420
Interest Period 0 1 2 3 418 419 420
![]()
![]()
![]()
![]()
![]() Payment
R R R R R R
Payment
R R R R R R
![]()
![]() R(1.005911931)-1
R(1.005911931)-1
![]() R(1.005911931)-2
R(1.005911931)-2
.
.
R(1.005911931)-418
![]()
![]() R(1.005911931)-419
R(1.005911931)-419
![]() R(1.005911931)-420
R(1.005911931)-420
This
forms the following geometric series:
R(1.005911931)-420 +
R(1.005911931)-419 + . . . + R(1.005911931)-2 +
R(1.005911931)-1
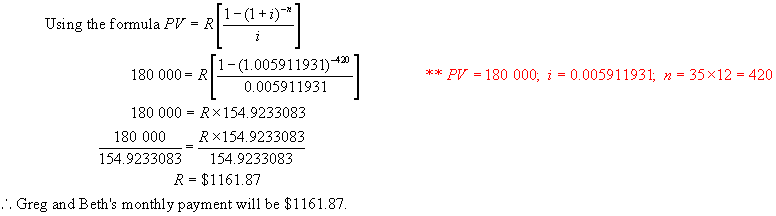
b)
Determine the total interest paid over the 25 year period.
Total amount repaid = 1013.85 x 300
= $304 095.00
Mortgage amount = $150 000
Interest paid = $304 095 - !50
000 =$154 095
Hence
The total interest paid over 25 years is $154 095.
2. In the question above, determine the
outstanding balance at the end of 10 years.
Solution:
Step 1: Using A = P(1 + i)n, find
the accumulated amount of $150 000 after 10 years at 0.5911931% per month
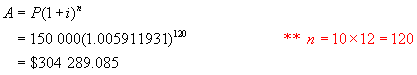
This is
the amount owing after 10 years if nothing was repaid.
Step 2: Find the amount of the annuity of
monthly payments of $1161.87 after 10 years at 0.5911931% per month.
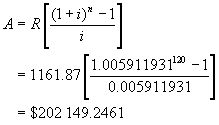
Step 3:
Subtract above 2 amounts to determine the amount still owing after 10
years.
$304 289.085 - $202 149.2461 = $102
139.84
Hence
$102 139.84 is still owing after 10 years.
The
chart below shows the amortization schedule through months 117 to 122. Note after 120 months or 10 years the amount
$102 139.84 is still owing.
Month Payment Interest Principal Balance
|
117 |
1161.87 |
616.85 |
545.02 |
103,794.32 |
|
118 |
1161.87 |
613.62 |
548.25 |
103,246.07 |
|
119 |
1161.87 |
610.38 |
551.49 |
102,694.59 |
|
120 |
1161.87 |
607.12 |
554.75 |
102,139.84 |
|
121 |
1161.87 |
603.84 |
558.03 |
101,581.81 |
|
122 |
1161.87 |
600.54 |
561.33 |
101,020.49 |
Note:
Interest
in month 118 calculated as follows: I
= $103 794.32 x 0.005911931 = $613.62
Principal P = $1161.87
- $613.62 = $548.25
Balance
(still owing) B = $103 794.32 - $548.25 =
$103 246.07
3. The Sturrocks purchased a cottage on Little
Straggle Lake for $140 000. They paid
25% down, financing the rest with a mortgage over 20 years with interest at
7.8%/a, compounded semi-annually.
a) Determine the monthly payment.
Solution:
Here the
payment interval( monthly ) is different than the interest period (
semi-annual). This is a general annuity.
We must
match the interest period to the payment interval.
Ie. We
must find the monthly rate that is equivalent to 7.8%/a, compounded
semi-annually.
Step 1:
Using the formula A = P(1 + i)n,
find the value of $1 invested at 7.8%/a, compounded semi-annually after 1 year.
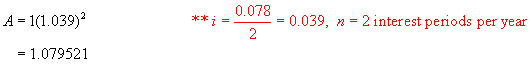
Step 2:
Let the equivalent monthly rate be i %. (Note the equivalent yearly rate would be 12i %.)
Now find the value of $1 invested at i % per month after 1 year.
A = 1(1 + i)12 ** n = 12, the number of times interest is
compounded per year.
Step 3:
These two amounts must be equal.
Hence
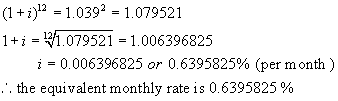
Down Payment
= 0.25 x $140 000 = $35 000
Mortgage
amount = $140 000 - $35 000 = $105 000.
The money in question is borrowed now – at
point 0 on the time line. Hence this is
a PV general annuity question
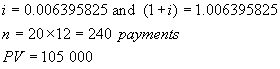
![]()
![]()
![]()
![]()
![]()
![]()
![]() Interest Period 0 1 2 3 238 239 240
Interest Period 0 1 2 3 238 239 240
![]()
![]()
![]()
![]()
![]() Payment
R R R R R R
Payment
R R R R R R
![]()
![]() R(1.006395825)-1
R(1.006395825)-1
![]() R(1.006395825)-2
R(1.006395825)-2
.
.
R(1.006395825)-238
![]()
![]() R(1.006395825)-239
R(1.006395825)-239
![]() R(1.006395825)-240
R(1.006395825)-240
This
forms the following geometric series:
R(1.006395825)-240 + R(1.006395825)-239
+ . . . + R(1.006395825)-2 + R(1.006395825)-1
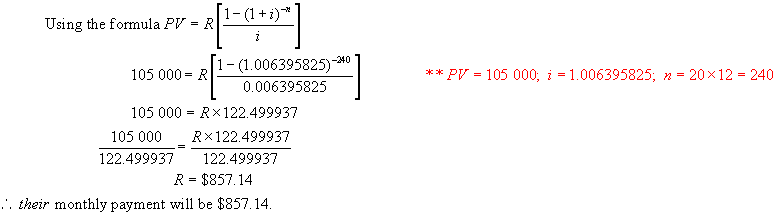
b) Determine the total interest paid over the
25 year period.
Total amount repaid = 857.14 x 240 =
$205713.60
Mortgage amount = $105 000
Interest paid = $205 713.60 - !05
000 = $100 713.60
Hence
the total interest paid over 20 years is $100 713.60.
4. In question 3 above, suppose the initial
term of the mortgage was 5 years at which time the terms are renegotiated.
a)
Find
the amount still owing at this time.
Solution:
Step 1: Using A = P(1 + i)n,
find the accumulated amount of $135 000 after 5 years at 0.6395825% per month
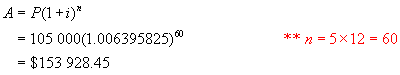
This is
the amount owing after 5 years if nothing was repaid.
Step 2: Find the amount of the annuity of
monthly payments of $857.14 after 5 years at 0.6395825% per month.
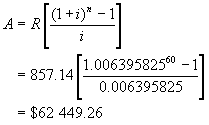
Step 3:
Subtract above 2 amounts to determine the amount still owing after 10
years.
$153 928.45 - $62 449.26 = $91
479.19
Hence
$91 479.19 is still owing after 5 years.
The
chart below shows the amortization schedule through months 57 to 62. Note after 60 months or 5 years the amount
$91 479.18 is still owing.
(difference
of $0.01 due to rounding in above solution).
Month Payment Interest Principal Balance
|
57 |
857.14 |
591.94 |
265.20 |
92,285.02 |
|
|
|
|
58 |
857.14 |
590.24 |
266.90 |
92,018.12 |
|
|
|
|
59 |
857.14 |
588.53 |
268.61 |
91,749.51 |
|
|
|
|
60 |
857.14 |
586.81 |
270.33 |
91,479.18 |
|
|
|
|
61 |
857.14 |
585.08 |
272.06 |
91,207.13 |
|
|
|
|
62 |
857.14 |
583.34 |
273.80 |
90,933.33 |
|
|
|
Note:
Interest
in month 60 calculated as follows: I =
$91 749.51 x 0.006395825 = $586.81
Principal P = $857.14
- $586.81 = $270.33
Balance
(still owing) B = $91 749.51 - $270.33 =
$91 479.18
b) Determine the new monthly payment to
maintain the mortgage if the rate changes to 8.4%/a, compounded semi-annually.
Solution:
We must
find the monthly rate that is equivalent to 8.4%/a, compounded semi-annually.
Step 1:
Using the formula A = P(1 + i)n,
find the value of $1 invested at 8.4%/a, compounded semi-annually after 1 year.
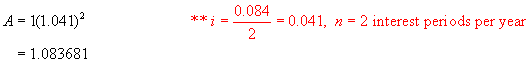
Step 2:
Let the equivalent monthly rate be i %. (Note the equivalent yearly rate would be 12i %.)
Now find the value of $1 invested at i % per month after 1 year.
A = 1(1 + i)12 ** n = 12, the number of times interest is
compounded per year.
Step 3:
These two amounts must be equal.
Hence
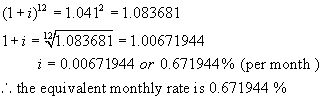
The money in question is borrowed now – at
point 0 on the time line. Hence this is
a PV general annuity with 15 years still to go.

![]()
![]()
![]()
![]()
![]()
![]()
![]() Interest Period 0 1 2 3 178 179 180
Interest Period 0 1 2 3 178 179 180
![]()
![]()
![]()
![]()
![]() Payment R R R R R R
Payment R R R R R R
![]()
![]() R(1.00671944)-1
R(1.00671944)-1
![]() R(1.00671944)-2
R(1.00671944)-2
.
.
R(1.00671944)-178
![]()
![]() R(1.00671944)-179
R(1.00671944)-179
![]() R(1.00671944)-180
R(1.00671944)-180
This
forms the following geometric series:
R(1.005911931)-180 +
R(1.005911931)-1799 + . . . + R(1.005911931)-2 +
R(1.005911931)-1
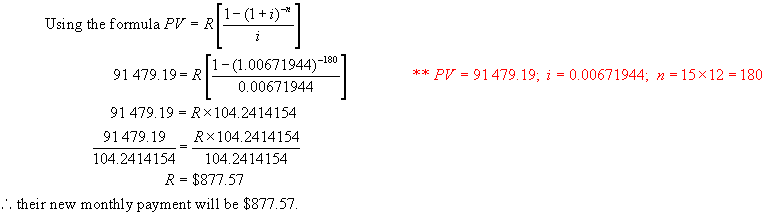
5 a)
Nora has just purchased a new home. For $220 000. If she will pay $100 000 down and mortgage
the rest it in weekly instalments over 20 years, find the weekly payment if the
interest rate is 7.2%/a, compounded semi-annually.
Solution:
We must
find the weekly rate that is equivalent
to 7.2%/a, compounded semi-annually.
Step 1:
Using the formula A = P(1 + i)n,
find the value of $1 invested at 7.2%/a, compounded semi-annually after 1 year.
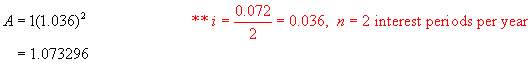
Step 2:
Let the equivalent weekly rate be i %. (Note the equivalent yearly rate would be 52i %.)
Now find the value of $1 invested at i % per week after 1 year.
A = 1(1 + i)52 ** n = 52, the number of times interest is
compounded per year.
Step 3:
These two amounts must be equal.
Hence
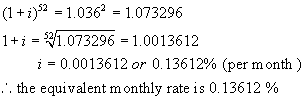
The money in question is borrowed now – at
point 0 on the time line. Hence this is
a PV general annuity with a term of 20 years.
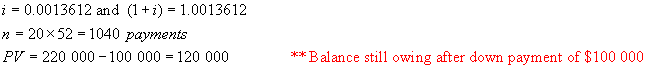
![]()
![]()
![]()
![]()
![]()
![]()
![]() Interest Period 0 1 2 3 1038 1039 1040
weeks
Interest Period 0 1 2 3 1038 1039 1040
weeks
![]()
![]()
![]()
![]()
![]() Payment
R R R R R R
Payment
R R R R R R
![]()
![]() R(1.0013612)-1
R(1.0013612)-1
![]() R(1.0013612)-2
R(1.0013612)-2
.
.
R(1.0013612)-1038
![]()
![]() R(1.0013612)-1039
R(1.0013612)-1039
![]() R(1.0013612)-1040
R(1.0013612)-1040
This
forms the following geometric series:
R(1.005911931)-1040 +
R(1.005911931)-1039 + . . . + R(1.005911931)-2 + R(1.005911931)-1

b) If she had chosen monthly payments at the
same rate, what would the payment be?
Solution:
We must
find the monthly rate that is
equivalent to 7.2%/a, compounded semi-annually.
Step 1:
Using the formula A = P(1 + i)n,
find the value of $1 invested at 7.2%/a, compounded semi-annually after 1 year.
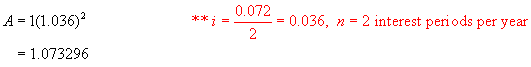
Step 2:
Let the equivalent monthly rate be i %. (Note the equivalent yearly rate would be 12i %.)
Now find the value of $1 invested at i % per month after 1 year.
A = 1(1 + i)12 ** n = 12, the number of times interest is
compounded per year.
Step 3:
These two amounts must be equal.
Hence
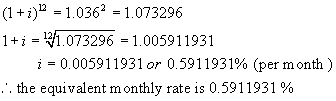
The money in question is borrowed now – at
point 0 on the time line. Hence this is
a PV general annuity with a term of 20 years.
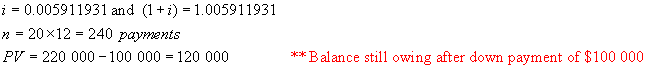
![]()
![]()
![]()
![]()
![]()
![]()
![]() Interest Period 0 1 2 3 238 239 240 months
Interest Period 0 1 2 3 238 239 240 months
![]()
![]()
![]()
![]()
![]() Payment
R R R R R R
Payment
R R R R R R
![]()
![]() R(1.005911531)-1
R(1.005911531)-1
![]() R(1.005911531)-2
R(1.005911531)-2
.
.
R(1.005911531)-238
![]()
![]() R(1.005911531)-239
R(1.005911531)-239
![]() R(1.005911531)-240
R(1.005911531)-240
This
forms the following geometric series:
R(1.005911931)-240 +
R(1.005911931)-239 + . . . + R(1.005911931)-2 +
R(1.005911931)-1