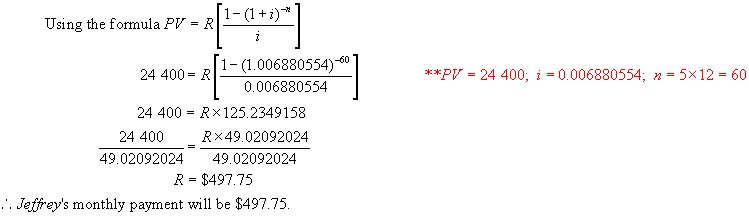|
|
|
|
|
||||||||
|
|
||||||||||||
|
|
UNIT
9 :
MATHEMATICS OF INVESTMENT
LESSON 5:
GENERAL ANNUITIES AND EQUIVALENT RATES
Definition: A general annuity is an annuity where the payment intervals are
not the same as the interest intervals.
Example 1:
Monthly payments of $500 where interest is 6%/a, compounded monthly. Here the payment
interval and the interest interval are the same – 1 month.
This is
an example of an ordinary annuity like those in previous lessons.
Suppose
there are monthly payments of $500, but the interest is 6%/a,
compounded semi-annually.
Here the payment interval is 1 month, but the interest period is 6
months. They are not the same. This type of annuity is called a general annuity.
Example 2:
Find the
amount of an annuity of $400 every 3 months ( ¼ year ) for 10 years if interest
is 8%/a, compounded annually.
Solution:
Here the
payment interval( ¼ year ) is different than the interest period (annual). This is a
general annuity.
We must
match the interest period to the payment interval.
Ie. We
must find the quarterly rate that is equivalent to 8%/a, compounded annually.
Step 1:
Using the formula A = P(1 + i)n,
find the value of $1 invested at 8%/a, compounded annually after 1 year.
A = 1(1.08)1
= 1.08
Step 2:
Let the equivalent ¼ year rate be i %. (Note the equivalent yearly rate would be 4i %.)
Now find the value of $1 invested at i % per ¼ year after 1 year.
A = 1(1 + i)4 ** n = 4, the number of times interest is
compounded per year.
Step 3:
These two amounts must be equal.
Hence
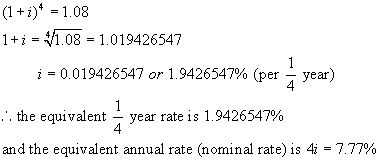
Now find
the amount of the annuity using the annuity formula.
Interest per. 0
1 2 . . . 118 119 120 Accumulated value
Payment 400 400 400 400 400
400
400(1.019426547)1
400(1.019426547)2
.
.
.
400(1.019426547)118
400(1.019426547)119
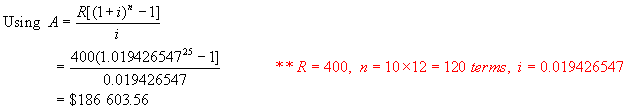
Hence the amount of the annuity is $186 603.56.
Example 3:
Find the
amount of an annuity of $700 every 6 months ( ½ year ) for 12 years if interest is 6%/a, compounded monthly.
Solution:
Here the
payment interval( ½ year ) is different
than the interest period (monthly).
This is a general annuity.
We must
match the interest period to the payment interval.
Ie. We
must find the semi-annual rate that is equivalent to 6%/a, compounded monthly.
Step 1:
Using the formula A = P(1 + i)n,
find the value of $1 invested at 6%/a, compounded monthly after 1 year.
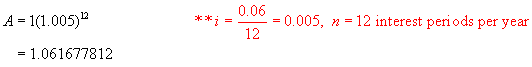
Step 2:
Let the equivalent ½ year rate be i %. (Note the
equivalent yearly rate would be 2i %.)
Now find the value of $1 invested at i % per ½ year after 1 year.
A = 1(1 + i)2 ** n = 2, the number of times interest is
compounded per year.
Step 3:
These two amounts must be equal.
Hence
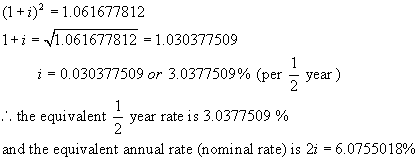
Now find
the amount of the annuity using the annuity formula.
Interest per. 0 1 2 . . . 22
23 24 Accumulated value
Payment 700 700 700 700 700
700
700(1.030377509)1
700(1.030377509)2
.
.
.
700(1.030377509)22
700(1.030377509)23
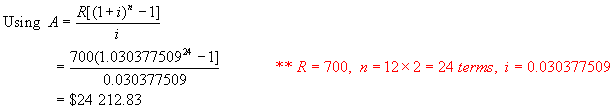
Hence the amount of the annuity is $24 212.83.
Example 4:
Find the
amount of an annuity of $2000 every year for 15 years if interest is 8%/a,
compounded quarterly.
Solution:
Here the
payment interval( 1 year ) is different than the interest period ( ¼
year). This is a general annuity.
We must
match the interest period to the payment interval.
Ie. We
must find the annual rate that is equivalent to 8%/a, compounded quarterly.
Step 1:
Using the formula A = P(1 + i)n,
find the value of $1 invested at 8%/a, compounded quarterly after 1 year.
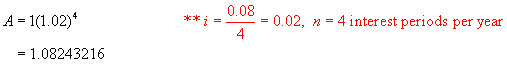
Step 2:
Let the equivalent annual rate be i %.
Now find the value of $1 invested at i % per year after 1 year.
A = 1(1 + i)1 ** n = 1, the number of times interest is
compounded per year.
Step 3:
These two amounts must be equal.
Hence
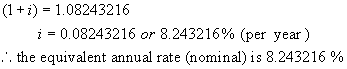
Now find
the amount of the annuity using the annuity formula.
Interest per. 0 1 2 . . . 13
14 15 Accumulated value
Payment 2000 2000 2000 2000
2000
2000
2000(1.08243216)1
2000(1.08243216)2
.
.
.
2000(1.08243216)13
2000(1.08243216)14
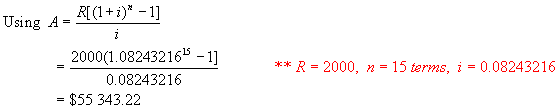
Hence the amount of the annuity is $55 343.22 .
Example 5:
Find the equivalent nominal (annual) interest rate, compounded annually for 6.6%/a, compounded semi-annually.
Solution:
Ie. We
must find the annual rate that is equivalent to 6.6%/a, compounded semi-annually.
Step 1:
Using the formula A = P(1 + i)n,
find the value of $1 invested at 6.6%/a, compounded semi-annually after 1 year.
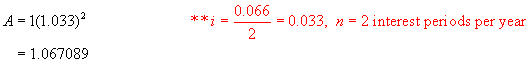
Step 2:
Let the equivalent annual rate be i %.
Now find the value of $1 invested at i % per year after 1 year.
A = 1(1 + i)1 ** n = 1, the number of times interest is
compounded per year.
Step 3:
These two amounts must be equal.
Hence
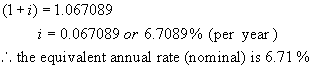
Example 6:
Find the equivalent nominal (annual) interest rate, compounded quarterly equivalent to 6.6%/a, compounded semi-aanually.
Solution:
Ie. We
must find the annual rate, compounded quarterly that is equivalent to 6.6%/a,
compounded semi-annually.
Step 1:
Using the formula A = P(1 + i)n,
find the value of $1 invested at 6.6%/a, compounded semi-annually after 1 year.
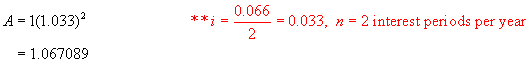
Step 2:
Let the equivalent ¼ year rate be i %. (Note the equivalent yearly rate would be 4i %.)
Now find the value of $1 invested at i % per ¼ year after 1 year.
A = 1(1 + i)4 ** n = 4, the number of times interest is
compounded per year.
Step 3:
These two amounts must be equal.
Hence
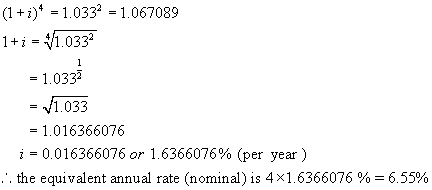
Example 7:
Jeffrey
has just purchased a new car for 24 400.
He borrows the money and will repay it in monthly instalments over 5
years. The interest rate is 8.4%/a,
compounded semi-annually. Find the
monthly payment.
Solution:
Here the
payment interval( monthly ) is different than the interest period (
semi-annual). This is a general annuity.
We must
match the interest period to the payment interval.
Ie. We
must find the monthly rate that is equivalent to 8.4%/a, compounded
semi-annually.
Step 1:
Using the formula A = P(1 + i)n,
find the value of $1 invested at 8.4%/a, compounded semi-annually after 1 year.
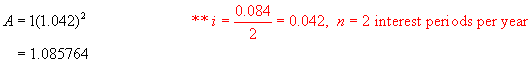
Step 2:
Let the equivalent monthly rate be i %. (Note the equivalent yearly rate would be 12i %.)
Now find the value of $1 invested at i % per month after 1 year.
A = 1(1 + i)12 ** n = 12, the number of times interest is
compounded per year.
Step 3:
These two amounts must be equal.
Hence
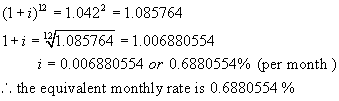
The money in question is borrowed now – at
point 0 on the time line. Hence this is
a PV general annuity question
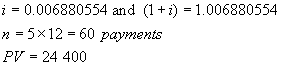
Interest Period 0 1 2 3 58 59 60
Payment
R R R R R R
R(1.006880554)-1
R(1.006880554)-2
.
.
R(1.006880554)-58
R(1.006880554)-59
R(1.006880554)-60
This
forms the following geometric series:
R(1.006880554)-60 +
R(1.006880554)-59 + . . . + R(1.006880554)-2 +
R(1.006880554)-1
