|
|
|
|
|
||||||||
|
|
||||||||||||
|
|
UNIT
9 :
MATHEMATICS OF INVESTMENT
LESSON 7:
UNIT 9 SUMMARY
Simple
Interest:
When you
borrow or invest money, interest is paid or earned. If the interest is calculated only on the money originally invested, it is called simple
interest.
![Text Box: I = interest due or earned
p = principal [amount borrowed
or invested]
t = time in years
r = yearly interest rate as a decimal
A = amount repayable or accumulated](./invrev_files/image002.gif)
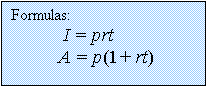
Compound
Interest:
If
interest is calculated at the end of each year (or interest period) and added
on at this point, then this is called compound
interest.
![Text Box: P = principal [amount borrowed
or invested]
n = number of interest periods
i = interest rate per interest period as
as a decimal
A = accumulated amount (due or payable)](./invrev_files/image004.gif)
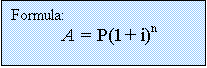
Time
Value of Money:
The
investment above can be illustrated on a time line. Time = 0 means today. The
arrow moving to the right shows the investment increasing over the 3 year
period.
0 1 2 3
$5000 $5000(1.05)3
Note: We can evaluate a give sum of money at any point using a
time line simply using the compound interest formula, the correct interest rate
and the correct number of time periods.
Example : Using different compounding periods.
a) Shelby invested $8 000 in a 5-year term
deposit which pays interest at a rate of 5 %/a [per annum], compounded
semi-annually. What will the investment
be worth at the end of the 5 year period?
Solution:
Because
the interest is compounded every 6 months, we must adjust both the number of
interest periods n and the interest rate i.
If
interest is paid twice a year, then the number of interest periods [compounding
periods] will be 5 x 2 = 10. Hence n
= 10.
The
appropriate time line is shown below.
Since there are 10 interest periods, we will put a mark every 6 months
over the 5-year period.
0 1 2 . .
. . . 4
5
…
$8000 $8000(1.025)10
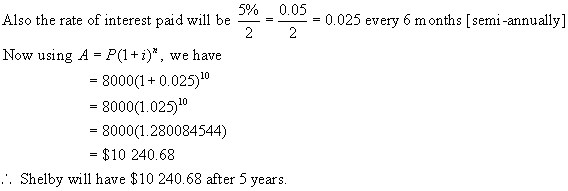
Present
Value:
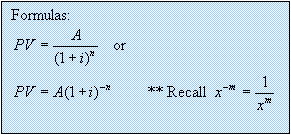
Example:
Mr. And
Mrs. Trinh would like to have $500 000 available when they retire in 20
years. How much should they invest now
if interest is 6%/a, compounded semi-annually?
Solution:
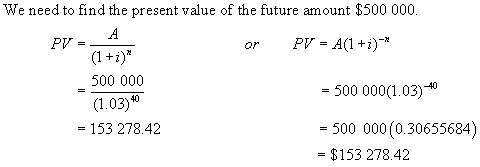
The
appropriate time line is shown below.
Since there are 40 interest periods, we will put a mark every 6 months
over the 20-year period.
0 1 2 3
4 . .
. 38
39 40
500000(1.03)-40 500000
They
should invest $153 278.42 today to achieve their goal.
Ordinary
Annuities:
Definition: A sequence
of payments made at
regular intervals is called an annuity.
Interest Period 0
1 2 3 18
19 20
Payment 200 200 200 200 200 200
An ordinary annuity has the following properties.
![Text Box: P = principal [amount borrowed
or invested]
n = number of interest periods
i = interest rate per interest period as
as a decimal
A = accumulated amount (due or payable)](./invrev_files/image050.gif)
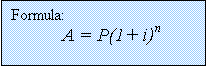
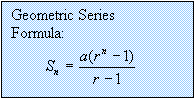
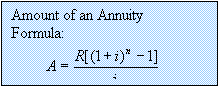
Example:
For the
past 5 years Amane has been depositing $100 every month into an investment
account . If the interest rate is
5.4%/a, compounded monthly, how much has she accumulated at the time of her last
deposit? Include a time line diagram in
your solution.
Solution:
$100 at
the end of every month for 5 years with interest at 4.25%/a, compounded
monthly.
Interest period0 1
2 . . . 238 239
240 Accumulated value
Payment 100 100 100 100 100
100
100(1.0045)1
100(1.0045)2
.
.
.
100(1.0045)59
100(1.0045)59
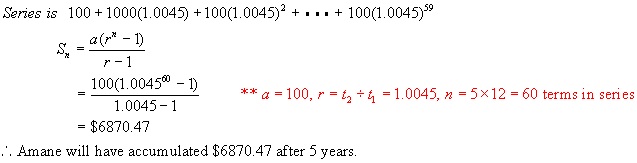
Example:
Find the
annual payment for an annuity of 10 years duration at a rate of 5.6%/a,
compounded annually, that will amount to $10 000 at the time of the last
payment.
Solution:
Let the
yearly payment be $R, with the first payment at the end of the first year; i
= 0.056 and 1 + i = 1.056
Interest period0 1
2 . . . 8
9 10 Accumulated value
Payment R R
R R R
R
R(1.056)1
R(1.056)2
.
.
.
R(1.056)8
R(1.056)9
Present
Value of an Annuity:
Definition 1: A sequence of payments made at regular
intervals is called an annuity.
Definition 2: When we calculate the present values of the
sequence of payments made at regular intervals this is called the Present
Value of the annuity.
A Present Value annuity has the following properties.
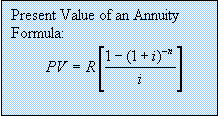
Example 1: Finding the Present Value of an annuity.
Heywood
recently won $5 000 000 in the lottery.
He plans to purchase an annuity that will pay him $50 000 every year for
25 years and spend the rest. How much
of his winnings would he need to pay today for that annuity if
interest is 7.6%/a, compounded annually? Include the series and a time line diagram in the solution.
Solution:
We
calculate the present values of the 25 future payments of $50 000 each. Notice the
arrows go to the left for a present value annuity.
Interest Period 0 1
2 3 23 24 25
Payment( 1000’s) 50 50 50 50 50
50000(1.076)-1
50000(1.076)-2
.
.
50000(1.076)-23
50000(1.076)-24
50000(1.076)-25
This
forms the following geometric series:
Note – write the last term first.
50
000(1.076)-25 + 50000(1.076)-24 + . . . + 50000(1.076)-2 +
50000(1.076)-1
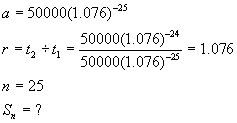
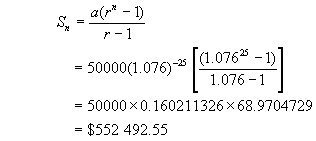
Hence
Michael needs $552 492.55
of his winnings to purchase the annuity. He would have $5 000 000 - $ 552
492.55 = $4 447 507.45 left to spend.
Alternate Solution:
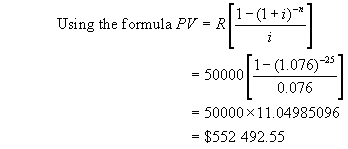
Notice
this present value amount is much less than the total amount paid out over 25
years which would be 25 x $50 000=$1 250 000.
General
Annuities:
Definition: An annuity where the payment intervals are not the same as the
interest intervals.
Example:
Find the
amount of an annuity of $700 every 6 months ( ˝ year ) for 12 years if interest is 6%/a, compounded monthly.
Solution:
Here the
payment interval( ˝ year ) is different
than the interest period (monthly).
This is a general annuity.
We must
match the interest period to the payment interval.
Ie. We
must find the semi-annual rate that is equivalent to 6%/a, compounded monthly.
Step 1:
Using the formula A = P(1 + i)n,
find the value of $1 invested at 6%/a, compounded monthly after 1 year.
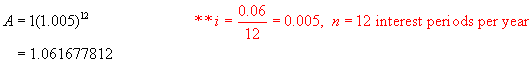
Step 2:
Let the equivalent ˝ year rate be i %. (Note the
equivalent yearly rate would be 2i %.)
Now find the value of $1 invested at i % per ˝ year after 1 year.
A = 1(1 + i)2 ** n = 2, the number of times interest is
compounded per year.
Step 3:
These two amounts must be equal.
Hence
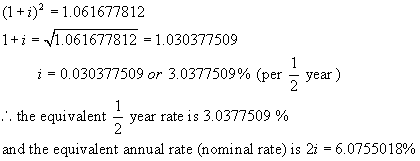
Now find
the amount of the annuity using the annuity formula.
Interest per. 0 1 2 . . . 22
23 24 Accumulated value
Payment 700 700 700 700 700
700
700(1.030377509)1
700(1.030377509)2
.
.
.
700(1.030377509)22
700(1.030377509)23
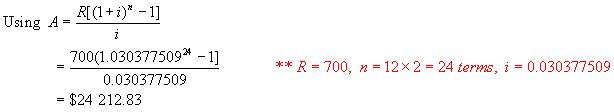
Hence the amount of the annuity is $24 212.83.
Mortgages:
Example 1:
a) Camille has just purchased a new house near
Brantford. She needs a mortgage of
$150 000 after her down payment.. She
will repay it in monthly instalments over 25 years. The interest rate is 6.6%/a, compounded semi-annually. Find the monthly payment.
b) Determine the total interest paid over the
25 year period.
Solution:
Here the
payment interval( monthly ) is different than the interest period (
semi-annual). This is a general annuity.
We must
match the interest period to the payment interval.
Ie. We
must find the monthly rate that is equivalent to 6.6%/a, compounded
semi-annually.
Step 1:
Using the formula A = P(1 + i)n,
find the value of $1 invested at 6.6%/a, compounded semi-annually after 1 year.
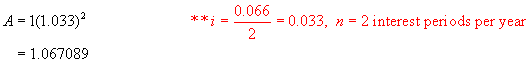
Step 2:
Let the equivalent monthly rate be i %. (Note the equivalent yearly rate would be 12i %.)
Now find the value of $1 invested at i % per month after 1 year.
A = 1(1 + i)12 ** n = 12, the number of times interest is
compounded per year.
Step 3:
These two amounts must be equal.
Hence
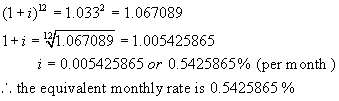
The money in question is borrowed now – at
point 0 on the time line. Hence this is
a PV general annuity question
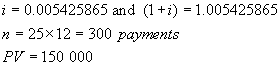
Interest Period 0 1 2 3 58 59 60
Payment
R R R R R R
R(1.005425865)-1
R(1.005425865)-2
.
.
R(1.005425865)-298
R(1.005425865)-299
R(1.005425865)-300
This
forms the following geometric series:
R(1.005425865)-300 +
R(1.005425865)-59 + . . . + R(1.005425865)-2 +
R(1.005425865)-1
b)
Determine the total interest paid over the 25 year period.
Total amount repaid = 1013.85 x 300
= $304 095.00
Mortgage amount = $150 000
Interest paid = $304 095 - !50
000 =$154 095
Hence
The total interest paid over 25 years is $154 095.