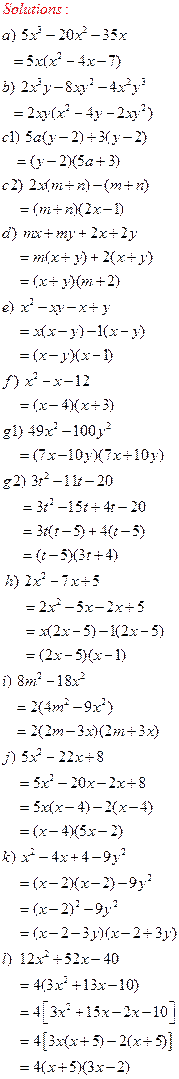|
|
|
|
|
|
||||||||||||
|
|
||||||||||||||||
UNIT 1 :
ALGEBRA PREP
LESSON 4: OPERATIONS WITH
POLYNOMIALS HOMEWORK QUESTIONS
HOMEWORK QUESTIONS:
1.
Expand and simplify:
a) (x2
– 3x + 4) + (4x2 – 2x + 5) b)
(x2 – 2x – 3) – (5x2 + 3x – 2)
c) (-3x2
+ 2x – 5) – 2x(3x – 4) + 3(x – 5) d)
3x2(2x3 – 6x – 2) – x(5x3 – 3x2 +
1)
2.
Expand and simplify:
a) 3[2x –
(x – 5)] –2x[5x – (3x – 2)] b)
(2x – 1)(3x2 – 5x – 2)
c) (x2
+ 2)(x2 – 5x + 3) d)
5(3 – 2x)(4x – 1) – 2x(3x + 2)2
e) (2a – 3)2(a
– 2) – 3a(a – 1)(4a + 2)
f) (5a – 1)(2a3 – 3a2 + a – 5)
g) (2a – 3b
+ c)3
3.
Expand and simplify:
![]()
![]()
4. Factor Fully:
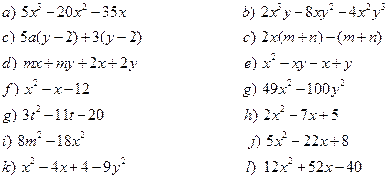
Solutions:
1.
Expand and simplify:
a) (x2
– 3x + 4) + (4x2 – 2x + 5) b)
(x2 – 2x – 3) – (5x2 + 3x – 2)
c) (-3x2
+ 2x – 5) – 2x(3x – 4) + 3(x – 5) d)
3x2(2x3 – 6x – 2) – x(5x3 – 3x2 +
1)
Solutions:
a) (x2 – 3x + 4) + (4x2 – 2x + 5) = x2 –
3x + 4 + 4x2 – 2x + 5
= 5x2 – 5x + 9
b) (x2
– 2x – 3) – (5x2 + 3x – 2) = (x2 – 2x – 3) – 1(5x2
+ 3x – 2)
= x2 – 2x – 3 – 5x2 –
3x + 2
= -4x2 – 5x – 1
c) (-3x2
+ 2x – 5) – 2x(3x – 4) + 3(x – 5) = -3x2 + 2x – 5 – 6x2 +
8x + 3x – 15
= -9x2 + 13x - 20
d) 3x2(2x3
– 6x – 2) – x(5x3 – 3x2 + 1) = 6x5 – 18x3
– 6x2 – 5x4 + 3x3 – x
=
6x5 – 5x4 – 15x3 – 6x2 – x
2.
Expand and simplify:
a) 3[2x –
(x – 5)] –2x[5x – (3x – 2)] b)
(2x – 1)(3x2 – 5x – 2)
c) (x2
+ 2)(x2 – 5x + 3) d)
5(3 – 2x)(4x – 1) – 2x(3x + 2)2
e) (2a – 3)2(a
– 2) – 3a(a – 1)(4a + 2)
f) (5a – 1)(2a3 – 3a2 + a – 5)
g) (2a – 3b
+ c)3
Solutions:
a) 3[2x –
(x – 5)] –2x[5x – (3x – 2)] = 3(2x – x + 5) – 2x(5x – 3x + 2)
=
3(x + 5) – 2x(2x + 2)
=
3x + 15 –4x2 – 4x
=
- 4x2 – x + 15
b) (2x –
1)(3x2 – 5x – 2) = 2x(3x2 – 5x – 2) – 1(3x2 –
5x – 2)
= 6x3 – 10x2 – 4x – 3x2
+ 5x + 2
= 6x3 – 13x2 + x + 2
c) (x2
+ 2)(x2 – 5x + 3) =
x2(x2 – 5x + 3) + 2(x2 – 5x + 3)
= x4
– 5x3 + 3x2 + 2x2 – 10x + 6
= x4
– 5x3 + 5x2 – 10x + 6
d) 5(3 –
2x)(4x – 1) – 2x(3x + 2)2 = 5(12x – 3 – 8x2 + 2x) – 2x(3x
+ 2)(3x + 2)
= 5(-8x2 + 14x – 3) – 2x(9x2
+ 6x + 6x + 4)
= -40x2 + 70x – 15 – 18x3
– 12x2 – 12x2 – 8x
= - 18x3 – 64x2 +
62x – 15
e) (2a – 3)2(a
– 2) – 3a(a – 1)(4a + 2) = (4a2
– 12a + 9)(a – 2) – 3a(4a2 – 2a – 2)
=
4a3 – 8a2 –12a2 + 24a + 9a – 18 – 12a3
+ 6a2 + 6a
=
-8a3 – 14a2 + 39a – 18
f) (5a – 1)(2a3 – 3a2 +
a – 5) = 5a(2a3 – 3a2 + a – 5) – 1(2a3 – 3a2
+ a – 5)
=
10a4 – 15a3 + 5a2 – 25a – 2a3 + 3a2
– a + 5
=
10a4 – 17a3 + 8a2 – 26a + 5
g) (2a – 3b
+ c)3 = (2a – 3b + c) (2a – 3b + c) (2a – 3b + c)
= (2a - 3b + c)(4a2 – 6ab + 2ac
–6ab +9b2 –3bc +2ac – 3bc +c2)
= (2a – 3b + c)(4a2 + 9b2
+ c2 –12ab + 4ac – 6bc)
= 8a3 + 18ab2 +2ac2
–24a2b +8a2c –12abc –12a2b – 27b3
–3bc2 +36ab2 –12abc + 18b2c + 4a2c
+9b2c +c3 – 12abc + 4ac2 –6bc2
= 8a3 – 27b3 + c3
+ 54ab2 +6ac2 –36a2b + 12 a2c – 9bc2
+ 27b2c –36abc
3.
Expand and simplify:
![]()
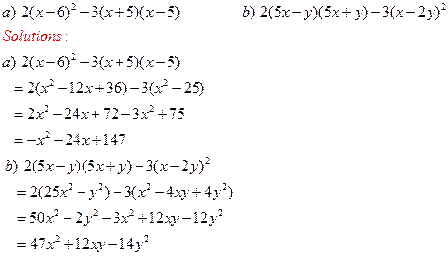
4. Factor Fully: