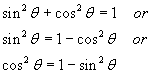|
|
|
|
|
||||||||
|
|
||||||||||||
LESSON 7:Review
& Summary

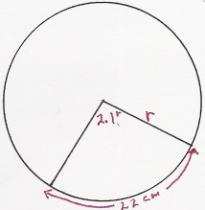
Relation between Radians and
degrees:
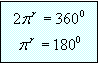
Example 1: Conversions from radian
measure to degree measure

Solution:
![]()
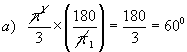
Example 2: Conversions from degree
measure to radian measure
![]()
Solution:
![]()
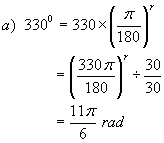
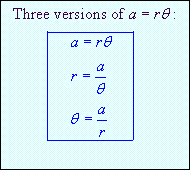
![]()
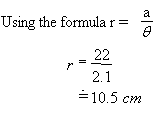
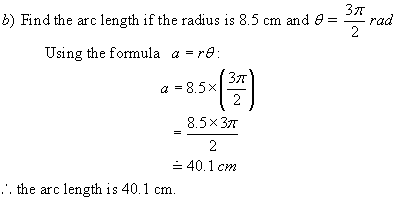
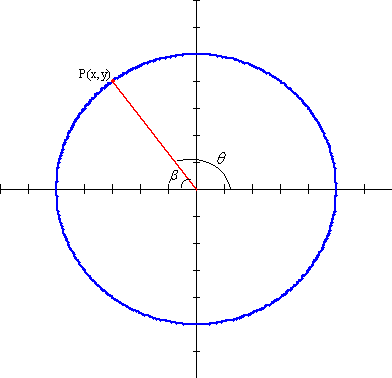
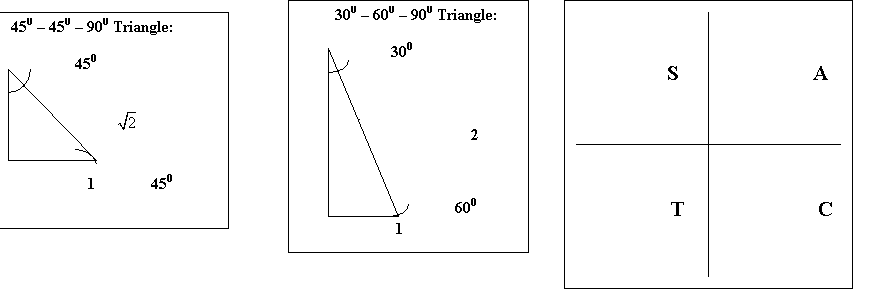
Angles in Standard Position:


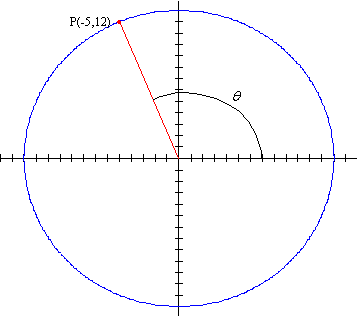
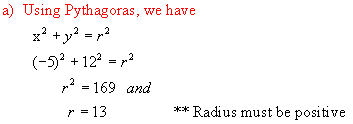
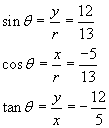
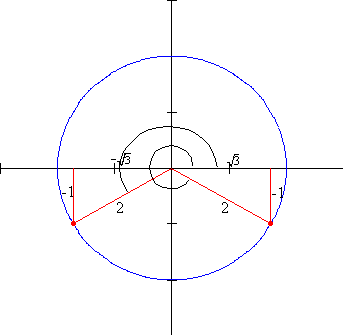
2. Find the exact value of :
![]()
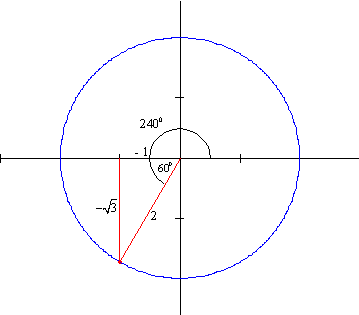

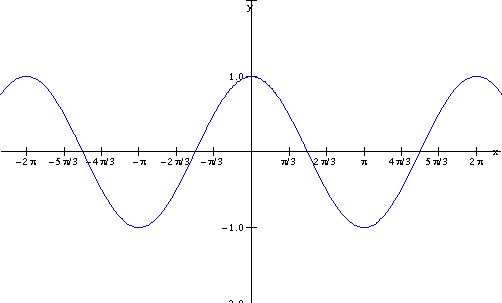
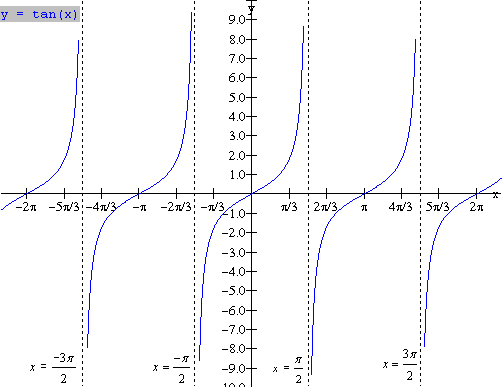
Graphs of Trig. Functions
![]()
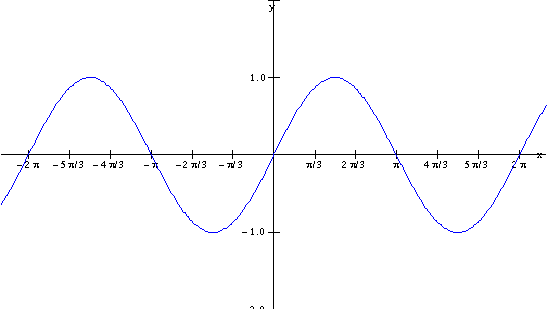
![]()
![]()
Combinations
of Transformations -- y = a sin k(x
– d) + c and y = a cos k(x – d) + c
Example 4: Sketch the graph of the basic
function ![]() Use transformations
to sketch
Use transformations
to sketch ![]() .
.
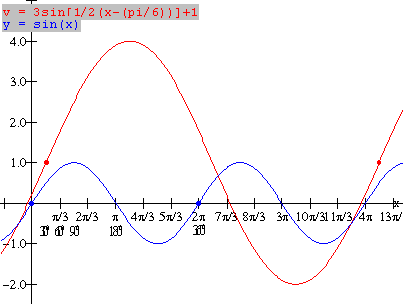
Solution: For ![]() , construct a table of values of key points and plot the
graph [blue]:
, construct a table of values of key points and plot the
graph [blue]:
|
x0 |
0 |
90 |
180 |
270 |
360 |
|
y |
0 |
1 |
0 |
-1 |
0 |

(x, y) -----------------------à (2x + 300, 3y + 1)
Using
the mapping and the points from the table above we get points for the
transformed graph
(x, y) -----------------------------à (2x + 300,
3y + 1)
(0, 0)
------------------------à (300, 1)
(900, 1)
----------------------à (2100, 4)
(1800, 0)
---------------------à (3900, 1)
(2700 , -1)
--------------------à (5700, -2)
(3600, 0) ----------------------à (7500, 1) [red graph at left]
In radians, the points (see table
at top of page) would be:
![]()
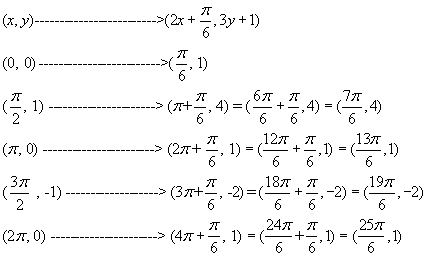
Amplitude: |a| =
3
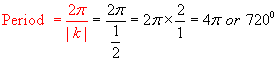
![]()
Domain of 1 period or cycle
(between red dots on graph):
![]()
Range: The maximum value of y is 4 and the
minimum value is –2
![]()
![Text Box: In summary, to graph y = a sin [k(x – d)] + c from the graph of y = sin(x), follow these ideas:
· If a < 0, we have a reflection in the x-axis
· If k < 0, we have a reflection in the y-axis
· If | a | < 1, we have a vertical compression , factor | a |
· If | a | > 1, we have a vertical stretch, factor | a |
·
· If | k | < 1, we have a horizontal stretch, factor 1/k
· If | k | > 1, we have a horizontal compression, factor 1/k
· The value of d gives the horizontal translation (phase shift)
· The value of c gives the vertical translation (shift)](./trig2rev_files/image077.gif)
Solving
Trig. Equations:
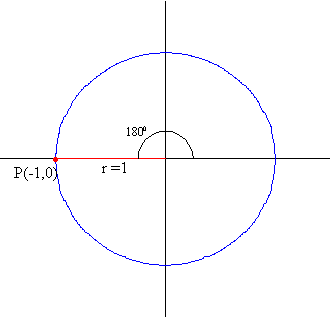
Example:
![]()
Solution:


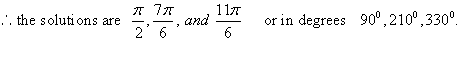
 Basic
Trigonometric Identities :
Basic
Trigonometric Identities :
1.
Quotient Identity:
![]()
2.
Pythagorean Identities: