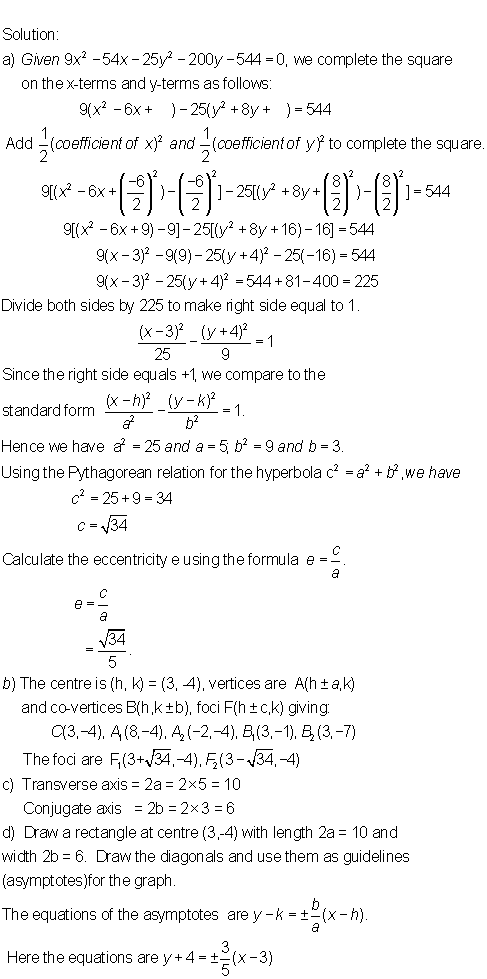Home

Locus

The Circle

The Ellipse

The Parabola

The Hyperbola

General Form

Intersections of Lines & Conics

Summary&Test

UNIT 10 : THE CONICS

LESSON 5: THE HYPERBOLA

Definition: Given two fixed points in the plane F₁ and F₂. A hyperbola is the locus (set) of points P such that the difference |PF₂ – PF₁ | is a constant. The two fixed points are the foci.

The centre is the midpoint of the line segment joining the two foci (F₁F₂).

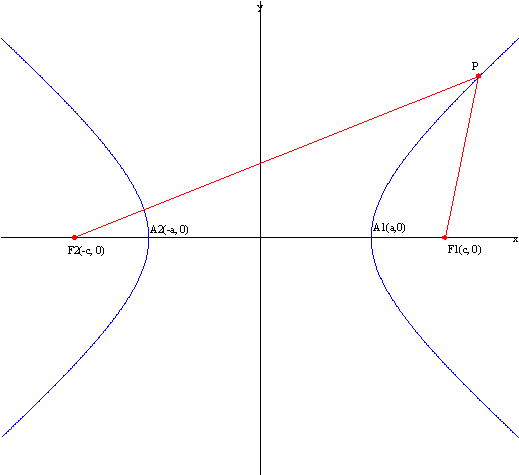
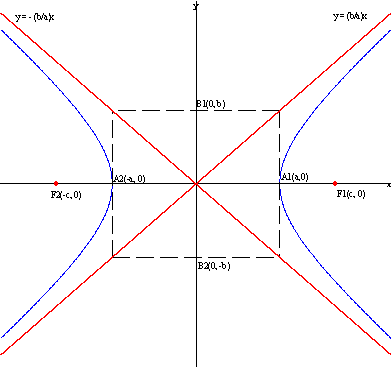
Hyperbola with foci on the x-axis:

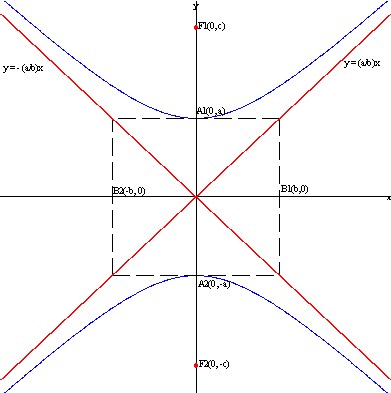
Hyperbola with foci on the y-axis:

Example 1:

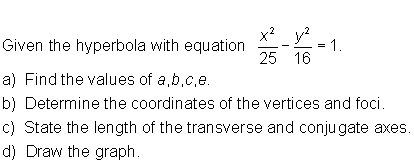
Solution:

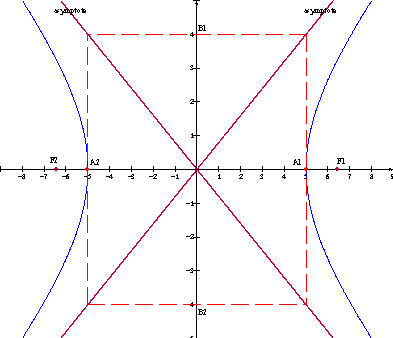
Example 2:

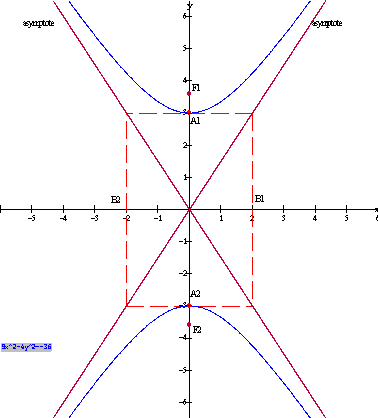
Given the hyperbola with equation 9x² - 4y² = - 36.

a) Put the equation in standard form and find the

values of a, b, c, e.

b) Determine the coordinates of the vertices.

c) State the length of the transverse and conjugate axes.

d) Find the equations of the asymptotes.

e) Draw the graph.

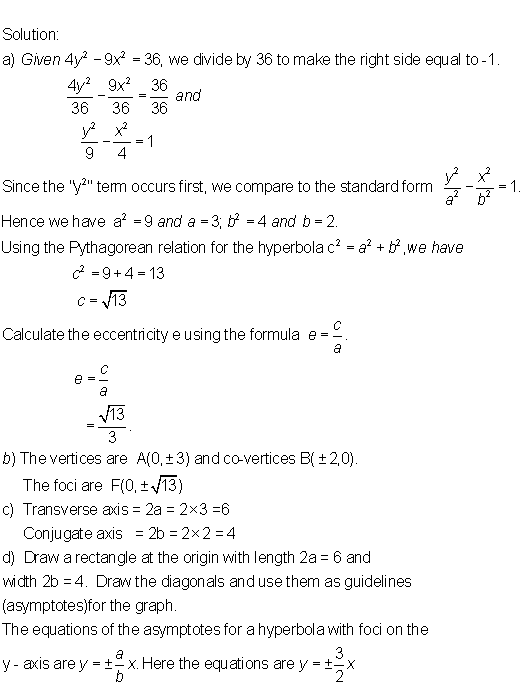
Example 3:

Solution:

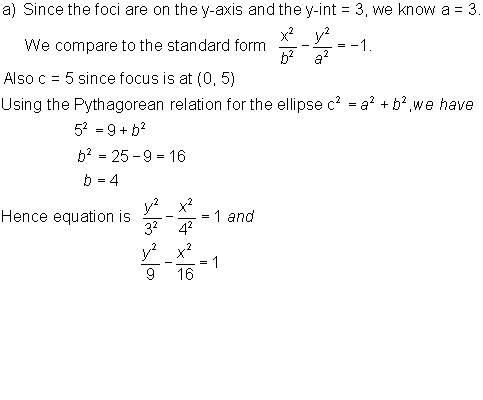
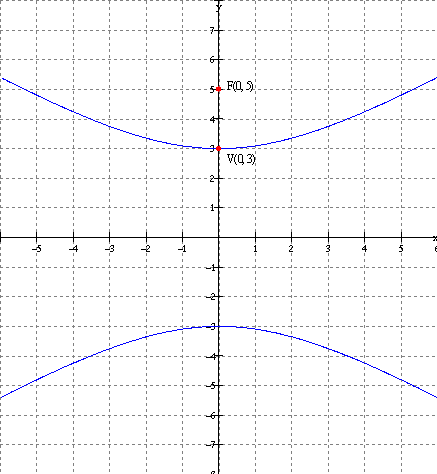
Example 4:

Given the hyperbola with equation 9x² –54x – 25y² + 200y – 544 = 0.

a) Put the equation in standard form and find the

values of a, b, c, e.

b) Determine the coordinates of the vertices.

c) State the length of the transverse and conjugate axes.

d) Find the equations of the asymptotes.

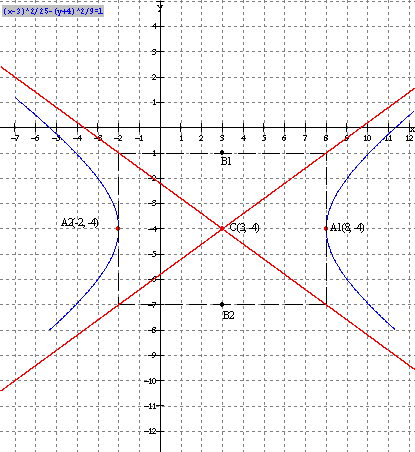
e) Draw the graph

Return to top of page

Click here to go to homework questions