jdlogo

jdlogo

jdlogo

jdlogo

jdlogo

Home

Right Triangles

Angles in Standard Position

Sine Law & Ambiguous Case

Cosine Law

Problem Solving

Summary&Test

 

jdsmathnotes

 

 


UNIT 6  : BASIC TRIGONOMETRY WITH TRIANGLES

 LESSON 6:  UNIT SUMMARY

 

Pythagorean Theorem:

In any right triangle, the square on the hypotenuse [c] equals the sum of the squares on the other two sides [a,b].

 

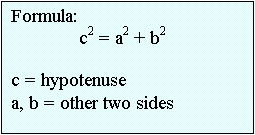
Text Box: Formula: c2 = a2 + b2 c = hypotenuse a, b = other two sides                        

 

                                          

 

      a          c

 

 

               b

 

 

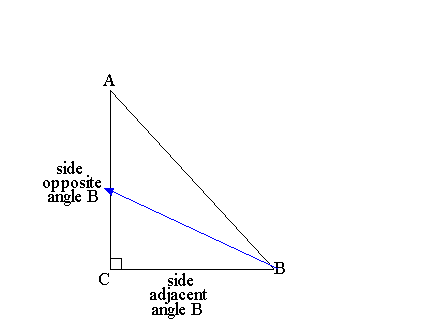
Primary Trigonometric Ratios :

Text Box:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Text Box: Note: A right triangle can be solved if you are given either 2 sides, in which case you can find one of the acute angles OR if you are given 1 side and 1 angle, in which case you can find another side.
 

 

 

 

 


Text Box: Note: Triangle convention for naming sides and angles. · a is the side opposite < A · b is the side opposite < B A · c is the side opposite < C b c C B a                        

 

 

 

 

 

 

 

 

 

 


Example : Right Triangles – Two Triangle Questions.

 

Find DG to the nearest tenth in the diagram below.

 

                                             D 

 

                                                 

                        54.2o                                               31.6o

                            E                                                      G

                                    9.7 cm    F

                                         

 

  

 

Angles in Standard Position:

 

Definition:   An angle is in standard position if it has its vertex at the origin and  initial arm along the positive x-axis.  The terminal arm is found by rotating the initial arm about the origin to a terminal position in one of the 4 quadrants.  The rotation is positive if it is in the counter – clockwise direction and negative if in the clockwise direction.

 

                       

 

 

 

 

 

 

 

 

 

 

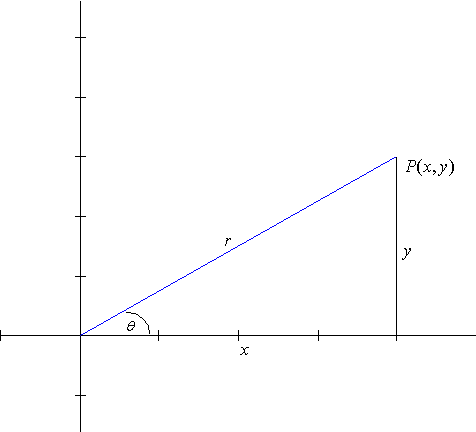
Example :

 

Solution:

 

x = 4

y = 3

r = 5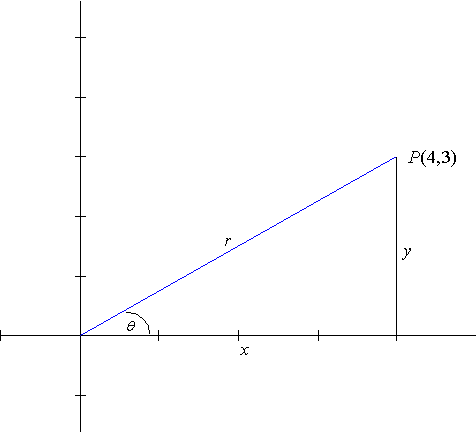

 
 
           

 

 

                                   

 

 

 

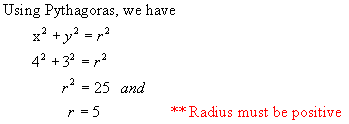
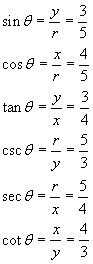
Example : Angles greater than 900   

 

Solution:

           

 

 

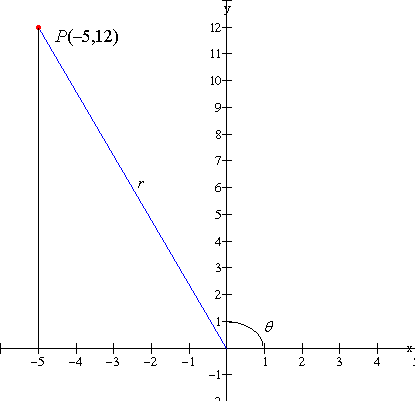
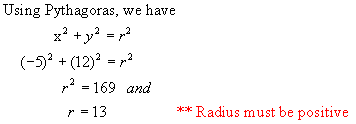
x = -5

y = 12

r = 13

 
 
                                   

 

 

 

 

 

 

 

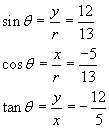
Note that sine is positive and cosine and tangent are negative for a second quadrant angle.

 

 

Result:  To find the trigonometric ratios of angles between 90o and 180o, use the following rules:

 

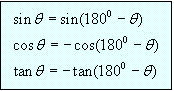
Text Box:
 

 

 

 

 

 

 

 


The Sine Law:

The sine law is used to solve oblique triangles, that is triangles which are not right angled.

 

                                                                                                                                           A

                                   

 

 

                                                                               c                                             b                                                       

 

 

 

                                                                                                                 B                             a                                           C

                                                                       

 

 

Text Box: Summary of main ideas: · Use the sine law when given 2 angles and a side (AAS) or two sides and a non-contained angle (SSA). · For the SSA situation, where the given angle is acute; the ambiguous case occurs if the side opposite the given angle is the shorter of the two given sides. (ex. 3(a) above) · To solve the triangle in this case, proceed as follows: 1. Calculate the height of the triangle (h = a sinB) 2. If b > h then there are two triangles 3. If b = h there is one right triangle 4. If b < h there is no triangle · For the SSA situation, where the given angle is acute; if the side opposite the given angle is the longer side, there is one solution. (ex. 2 above) · For the SSA situation, where the given angle is obtuse; if the side opposite the given angle is the longer side, there is one solution. (ex. 4(a) above) · For the SSA situation, where the given angle is obtuse; if the side opposite the given angle is the shorter side, there is no solution · For the AAS situation, there is one solution.
 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


 

           

                                            C                                                

 

 

 

               9.6                h            9.6           12.4          

 

 

 

                A1                                                                          420      B

                                                                           A2                                          

 

The Cosine Law:

The cosine law is  also used to solve oblique triangles, that is triangles which are not right angled.

It is used in the following two situations.

 

1.  Given two sides and a contained angle (SAS),  use one of the following 3 formulas to find the third side.

         

 

Text Box: The Cosine Law:
 

 

 

 


                                                                                                                  

 

 

2.  Given  three sides  (SSS), use one of the following 3 formulas to find an angle.

         

Text Box: The Cosine Law:
 

 

 

 


                                                                                                                  

 

 

 

 

 

 

 

 

Return to top of page

Click here to go to test questions