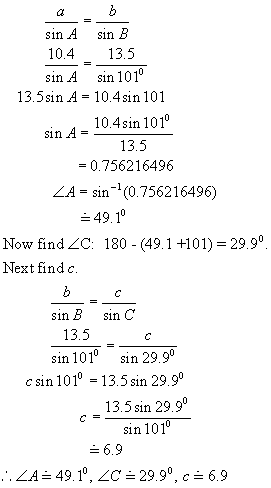|
|
|
|
|
|||||||
|
|
|||||||||||
UNIT 6 : BASIC
TRIGONOMETRY WITH TRIANGLES
LESSON
3: SINE LAW
The
Sine Law:
The sine
law is used to solve oblique triangles, that is triangles which are not right angled.
A
c b
B a C
Given
two angles and a side (AAS case)
Example 1:
A
c b
B 48o 29o C
22.4 cm
Solution:
First
find the measure of < A: 180o – (48o + 29o)
= 103o
Now find
c using the sine law:
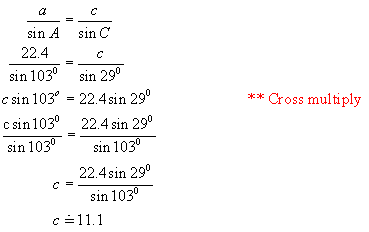
Now find
b using the sine law:
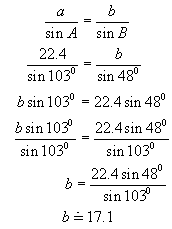
Given
two sides and an ACUTE angle (< 900) opposite one of the sides
[the non-contained angle] (SSA)
Example 2:
Note:
Here the longer side (23.1) is opposite the given acute angle < E is
acute. There is only one triangle in this case.
D
16.4 cm 23.1 cm
E 56.4o F
Solution:
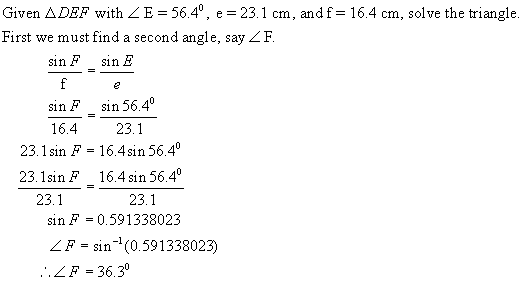
Now find
< D: 180 – (56.40 + 36.30)
= 87.30
Next
find d using the sin law:
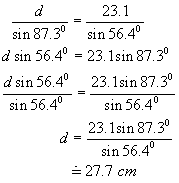
Given
two sides and an ACUTE angle where the shorter side (b) is opposite the given angle
(<
B) (SSA)
Example 3:
Solution: There are 3
possibilities here,
one of which is the so-called ambiguous case where there are two triangles
which satisfy the given conditions.
C
b a
A ( B
C
b h a
A ( B
D
C
b h b
a
A1 ( B
D A2
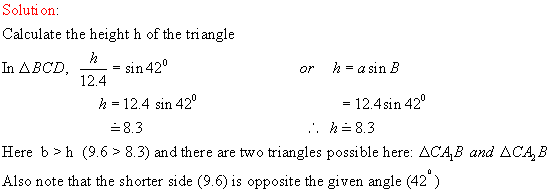
C
9.6 h 9.6
12.4
A1 420 B
A2
Hence there are two triangles to
solve here.
Triangle 1:
C
9.6 12.4
A1 420 B
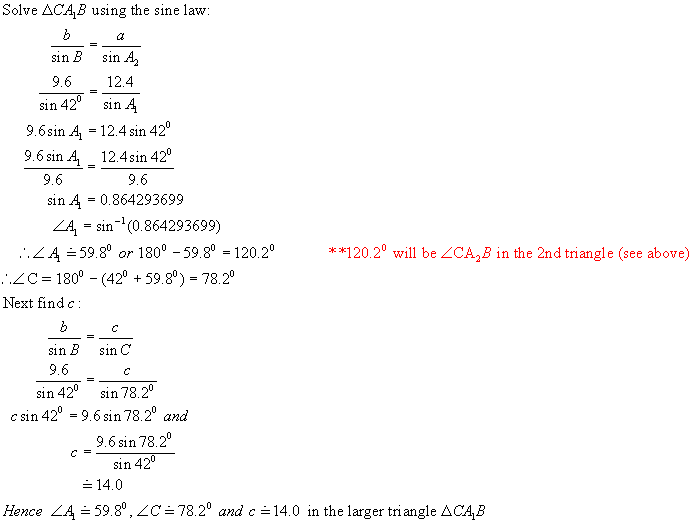
Triangle 2 : Recall from above that < CA2B = 120.20
C
9.6 12.4
A2 120.20 420
B
C
b=h a
A B
C
b h b
a
A A
( B
The
SSA case where the given angle B is OBTUSE (> 900)
Example 4:
C
b a
A B
C
b a
A B
Example 4(a):
C
13.5 10.4
A B
1010
Solution: This is the SSA case
with a given obtuse angle and the side opposite this angle is the
longer side.
There will
be only one triangle to solve.
First
find < A using the sine law.
